UERJ 2018 - Matemática

UERJ 2018 - 1º Exame de Qualificação

Questão 31

Onça e libra são unidades de massa do sistema inglês. Sabe-se que 16 onças equivalem a 1 libra
e que 0,4 onças é igual a x libras. O valor de x é igual a:
(A) 0,0125
(B) 0,005
(C) 0,025
(D) 0,05

Resolução

Sabendo que esses dois valores monetários são proporcionais, temos:

\frac{16}{1}=\frac{0,4}{x}

16\cdot x = 0,4

x = \frac{0,4}{16}

x = 0,025

Questão 32

Considere na imagem abaixo:

• os quadrados ACFG e ABHI, cujas áreas medem, respectivamente, S1 e S2;
• o triângulo retângulo ABC;
• o trapézio retângulo BCDE, construído sobre a hipotenusa BC, que contém o ponto X.

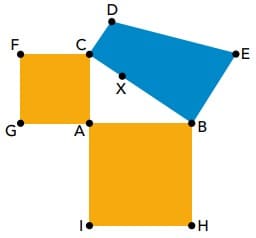
Sabendo que CD = CX e BE = BX, a área do trapézio BCDE é igual a:

(A) $\frac{S_1+S_2}{2}$

(B) $\frac{S_1+S_2}{3}$

(D) $\sqrt{{(S_1)}^2+{(S_2)}^2}$

Resolução 1

A maneira mais prática de resolver essa questão é através de uma das demonstrações do teorema de Pitágoras. Na figura, vemos que os dois catetos já estão associados a um quadrado, enquanto a hipotenusa está associada a um trapézio. O raciocínio se baseia em transformar esse trapézio em um quadrado duplicando a sua área. Sendo a área desse quadrado igual ao dobro da área do trapézio, ou seja, $2(S_3)$ :

S_1+S_2=2S_3

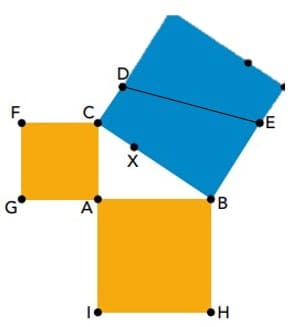
Portanto, a área do trapézio é:

S_3=\frac{S_1+S_2}{2}

Resolução 2

A segunda maneira é partindo da fórmula da área de um trapézio.

A_t=\frac{(B+b)h}{2}

Tomando $\overline{BE}$ e $\overline{CD}$ como bases, temos $\overline{BC}$ como altura.

A_t=\frac{(\overline{BE}+\overline{CD})\overline{CB}}{2}

Pelo enunciado, vemos que $\overline{CB}=\overline{BE}+\overline{CD}$ , já que $\overline{CX}=\overline{CD}$ e $\overline{BX}=\overline{BE}$

A_t=\frac{(\overline{BE}+\overline{CD})(\overline{BE}+\overline{CD})}{2}

A_t=\frac{{(\overline{CB})}^2}{2}

Pelo teorema de Pitágoras, temos:

{\overline {AC}}^2+{\overline {AB}}^2={\overline {CB}}^2

Portanto:

A_t=\frac{{\overline {AC}}^2+{\overline {AB}}^2}{2}

Por sua vez, o quadrado do lado representa a área da figura geométrica.

A_t=\frac{S_1+S_2}{2}

Questão 33

Os veículos para transporte de passageiros em determinado município têm vida útil que varia entre 4 e 6 anos, dependendo do tipo de veículo. Nos gráficos está representada a desvalorização de quatro desses veículos ao longo dos anos, a partir de sua compra na fábrica

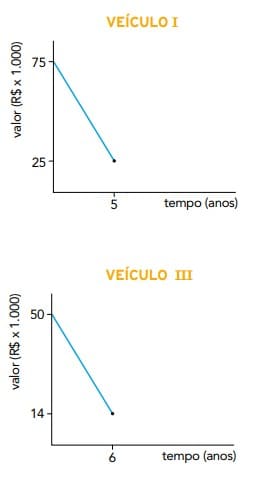
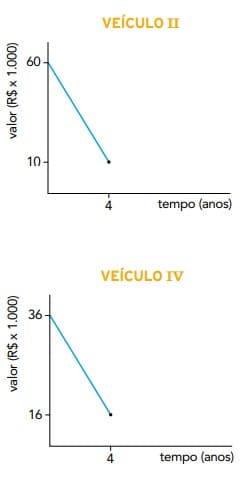
Com base nos gráficos, o veículo que mais desvalorizou por ano foi:

(A) I

(B) II

(D) IV

Resolução

A desvalorização é dada pela variação do preço do produto no tempo, logo:

d=\frac{V_f-V_i}{t}

(I)\; d=\frac{25-75}{5}= -10

(II)\; d=\frac{10-60}{4}=-12,5

(III)\; d=\frac{14-50}{6}=-6

(IV)\; d=\frac{16-36}{4}=-5

Alternativa correta – Letra B

Questão 34

As farmácias W e Y adquirem determinado produto com igual preço de custo. A farmácia W vende esse produto com 50% de lucro sobre o preço de custo. Na farmácia Y, o preço de venda do produto é 80% mais caro do que na farmácia W. O lucro da farmácia Y em relação ao preço de custo é de:
(A) 170%
(B) 150%
(C) 130%
(D) 110%

Resolução

Confira como resolver acrécimos e descontos.

Já que a farmácia W vende com 50% de lucro, então ela vende por:

P_v=P_c(1+0,5)

E o preço de venda da farmácia é Y é 80% maior.

P_v=P_c(1+0,5)(1+0,8)

P_v=P_c(2,7)

P_v=P_c(1+1,7)

P_v=P_c(100\% + 170\%)

Alternativa correta – Letra A

Questão 35

Admitindo um retângulo cujos lados medem a e b, sendo a < b, é possível formar uma sequência ilimitada de retângulos da seguinte forma: a partir do primeiro, cada novo retângulo é construído acrescentando-se um quadrado cujo lado é igual ao maior lado do retângulo anterior, conforme ilustrado a seguir.

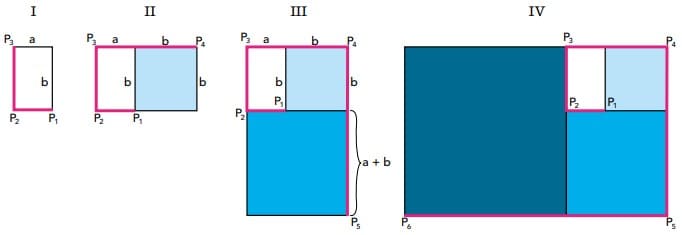
A figura IV destaca a linha poligonal $P_1P_2P_3P_4P_5P_6$ , formada pelos lados dos retângulos, que são os elementos da sequência $(a, b, a + b, a + 2b, 2a + 3b)$ . Mantendo o mesmo padrão de construção, o comprimento da linha poligonal $P_1P_2P_3P_4P_5P_6P_7$ , de $P1$ até o vértice $P7$ , é igual a:

(A) 5a + 7b

(B) 8a + 12b

(D) 21a + 33b

Resolução

A partir da sequência, vemos que, a partir do terceiro termo, cada termo representa a soma dos dois termos anteriores. Por isso, o comprimento da linha que vai até o vértice $P_7$ é a soma dos termos já presentes na sequência, mais os dois últimos termos.

L=(a+b+a+b+a+2b+2a+3b)+(a+2b+2a+3b)

L=8a+12b

Alternativa correta – Letra B

Questão 36

Cinco cartas de um baralho estão sobre uma mesa; duas delas são Reis, como indicam as imagens.

Após serem viradas para baixo e embaralhadas, uma pessoa retira uma dessas cartas ao acaso e, em seguida, retira outra. A probabilidade de sair Rei apenas na segunda retirada equivale a:

(A)\;\frac{1}{2}

(B)\;\frac{1}{3}

(C)\;\frac{2}{5}

(D)\;\frac{3}{10}

Resolução

Pelo enunciado, sabemos que a primeira carta retirada não deve ser o rei, ou seja, deve ser uma das outras 3.

P_1=\frac{3}{5}

E é dito que a segunda carta deve ser um Rei, lembrando que sobram apenas 4 cartas.

P_2=\frac{2}{4}=\frac{1}{2}

A probabilidade das duas acontecerem simultaneamente é:

P=\frac{3}{5} \cdot \frac{1}{2}

P=\frac{3}{10}

Alternativa correta – Letra D

2º Exame de Qualificação

Questão 30

Uma herança foi dividida em exatamente duas partes: x, que é inversamente proporcional a 2, e y, que é inversamente proporcional a 3. A parte x é igual a uma fração da herança que equivale a:

(A)\;\frac{3}{5}

(B)\;\frac{2}{5}

(C)\;\frac{1}{6}

(D)\;\frac{5}{6}

Resolução

X é inversamente proporcional a 2 e y é inversamente proporcional a 3, assim como x e y são diretamente proporcionais, pois a soma dos dois representa o todo.

\frac{x}{y}=\frac{\frac{1}{2}}{\frac{1}{3}}

\frac{x}{y}=\frac{1}{2} \cdot \frac{3}{1}

\frac{x}{y}=\frac{1}{2} \cdot \frac{3}{1}

\frac{x}{y}=\frac{3}{2}

Isolando o valor de y.

y=\frac{2x}{3}

Sabendo que a soma dos dois forma 100%.

x+y=1

Substituindo na equação acima.

x+\frac{2x}{3}=1

\frac{5x}{3}=1

x=\frac{3}{5}

Alternativa correta – Letra A

Questão 31

No triângulo equilátero ABC, H corresponde ao ponto médio do lado AC. Desse modo, a área do triângulo ABH é igual à metade da área de ABC.

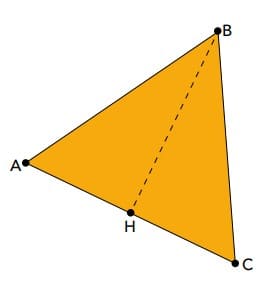
Sendo W o perímetro do triângulo ABH e Y o perímetro do triângulo ABC, uma relação correta entre W e Y é:

(A) $0 < W < \frac{Y}{2}$

(B) $W = \frac{Y}{2}$

(D) $W = Y$

Resolução

Para resolver essa questão, iremos testar separadamente cada possiblidade.

O perímetro W é dado por:

W=\overline{AH}+\overline{AB}+\overline{BH}

e $\overline{AH}$ é metade do segmento $\overline{AC}$

W=\frac{\overline{AC}}{2}+\overline{AB}+\overline{BH}

Somando os lados do triângulo, temos:

Y=\overline{AC}+\overline{AB}+\overline{BC}

\frac{Y}{2}=\frac{\overline{AC}}{2}+\frac{\overline{AB}}{2}+\frac{\overline{BC}}{2}

Sabemos que todos lados possuem o mesmo tamanho, por isso, $\frac{Y}{2}=1,5l$ , na medida que $W =1,5l +\overline{BH}$ . Logo:

W>\frac{Y}{2}

E, sabendo que Y corresponde a 3 lados e $\overline{BH}$ não é maior que 1,5l, deduzimos que:

Y>W

Y>W>\frac{Y}{2}

Alternativa correta – Letra C

Questão 32

No mapa mensal de um hospital, foi registrado o total de 800 cirurgias ortopédicas, sendo 440 em homens, conforme os gráficos abaixo.

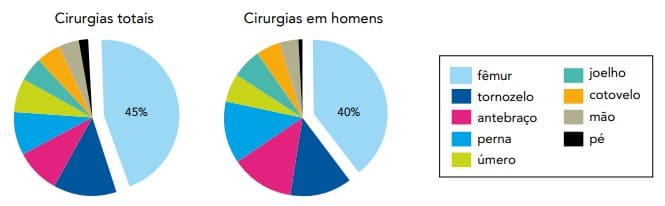
De acordo com esses dados, o número total de cirurgias de fêmur realizadas em mulheres foi:

(A) 144

(B) 162

(D) 190

Resolução

45% das cirurgias totais foram de fêmur, ou seja:

800\cdot 0,45=360

40% das cirurgias em homens foram de fêmur, isto significa:

440\cdot 0,4=176

Portanto, o número total de cirurgias de fêmur realizadas em mulheres foi:

360-176=184

Alternativa correta – Letra C

Questão 33

A imagem a seguir ilustra um prisma triangular regular. Sua aresta da base mede b e sua aresta lateral mede h.

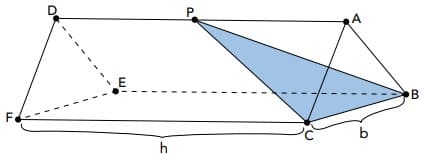
Esse prisma é seccionado por um plano BCP, de modo que o volume da pirâmide ABCP seja exatamente $\frac{1}{9}$ do volume total do prisma. Logo, a medida de $\overline{AP}$ é igual a:

(A) $\frac{h}{9}$

(B) $\frac{h}{3}$

(D) $\frac{5h}{6}$

Resolução

Sabendo que o volume pirâmide representa $\frac{1}{9}$ do volume do prisma:

V_{pirâmide}=\frac{V_{prisma}}{9}

Substituindo pelas suas respectivas fórmulas e admitindo que a base será a área lateral do prisma, temos:

\frac{A_{base}\cdot \overline{AP}}{3}=\frac{A_{base} \cdot h}{9}

Isolando o valor de $\overline{AP}$

\overline{AP}=\frac{3\cdot A_{base} \cdot h}{A_{base} \cdot 9}

\overline{AP}=\frac{h}{3}

Alternativa correta – Letra B

Questão 34

Um jogo consiste em lançar cinco vezes um dado cúbico, cujas faces são numeradas de 1 a 6, cada uma com a mesma probabilidade de ocorrer. Um jogador é considerado vencedor se obtiver pelo menos três resultados pares. A probabilidade de um jogador vencer é:

(A) $\frac{3}{5}$

(B) $\frac{2}{3}$

(D) $\frac{1}{2}$

Resolução

O que vamos fazer é calcular o número permutações onde o jogador vence, ou seja, as que apresentam 3 ou mais ocorrências de números e pares e depois associa-las às suas probabilidades.

3 pares e 2 ímpares

Temos aqui uma permutação com repetições onde se repetem 3 números pares e dois ímpares, logo:

P_5^{3,2}=\frac{5!}{3!2!}

P_5^{3,2}=\frac{5\cdot 4 \cdot 3!}{3!2!}

P_5^{3,2}=\frac{20}{2}=10

4 pares e 1 ímpar

P_5^{4}=\frac{5!}{4!}=5

5 pares

P_5^{5}=\frac{5!}{5!}=1

Sabendo que todos os números tem a mesma probabilidade de ocorrer, há 50% de chance do primeiro ser par, assim como há 50% dos demais serem pares. Pensando nisso, multiplicamos as chances referentes a cada lançamento para então multiplicar pelas permutações.

(P_5^{3,2}+P_5^{4}+P_5^{5}){(\frac{1}{2})}^5

=(16)(\frac{1}{32})

=\frac{16}{32}

=\frac{1}{2}

Alternativa correta – Letra D

Questão 34

Considere a sequência $(a_n)= (2, 3, 1, - 2, \dots)$ , n ∈ IN*, com 70 termos, cuja fórmula de recorrência é:

a_n=a_{n-1}-a_{n-2}

O último termo dessa sequência é:

(A) 1

(B) 2

(D) − 2

Resolução

Completando a sequência, temos:

(2,3,1,-2,-3,-1,2,3,\dots)

Averiguamos que após o 6º termo, a sequência volta a se repetir. Portanto, o resto dado pela divisão entre o número de termos e os número de termos a partir de onde a sequência volta a se repetir representa o termo que buscamos.

70 = 6(11) + 4

Sendo o resto igual a 4, o último termo da sequência é igual ao 4º da sequência, ou seja, -2.

Alternativa correta – Letra D

1 - Provas e gabaritos UERJ.

2 - Seção Enem

Além dos

Cálculos

Além dos

Cálculos

UERJ 2018 - Matemática

UERJ 2018 - 1º Exame de Qualificação

2º Exame de Qualificação

Conheça as nossas redes Sociais!

Para os amantes das exatas!