Questão 61.
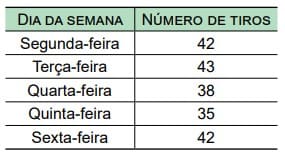
A tabela apresenta o número de tiros que uma pessoa deu nos 5 dias que treinou em um clube de tiros.
Naquela semana, a média aritmética diária de tiros que essa pessoa deu, nesse clube, foi:
(A) 38
(B) 39
(C) 40
(D) 41
(E) 42
Resolução
Sabendo que a média aritmética é igual a razão entre o somatório dos termos e o número de termos, temos:
\frac{42+43+38+35+42}{5}
=\frac{200}{5}
=40
Ou seja, essa pessoa deu 40 tiros em média por dia.
Alternativa correta – Letra C
Questão 62
Sobre um mapa de uma região, foi aplicado um sistema de coordenadas cartesianas, em que cada segmento de medida
unitária, nesse sistema, correspondia a 1,5 quilômetros reais e, nesse sistema, duas praças foram identificadas com as coordenadas (1, –3) e (4, 1). A distância real, em linha reta, em quilômetros, entre essas praças é de
(A) 5,0
(B) 5,5
(C) 6,0
(D) 7,5
(E) 8,0
Resolução
A distância entre dois pontos é dada pelo teorema de Pitágoras, onde os catetos são as diferenças nos eixos x e y.
D = \sqrt{{(1-4)}^2+{(-3-1)}^2}
D = \sqrt{{(-3)}^2+{(-4)}^2}
D = \sqrt{9+16}
D = \sqrt{25}
D = 5
Como cada unidade no plano representa 1,5km na vida real, basta multiplicarmos os dois valores.
D_r = 5 \cdot 1,5km
D_r = 7,5km
Alternativa Correta – Letra D
Questão 63
Em uma estrada, há telefones SOS instalados a cada 3 quilômetros, sendo o primeiro instalado no quilômetro 5. Do quilômetro 21 ao quilômetro 99, o número de telefones instalados
nessa estrada é
(A) 32
(B) 30
(C) 28
(D) 26
(E) 24
Resolução
Após o quilômetro 21, o primeiro telefone está instalado no km 23. Para saber quanto telefones estão situados dentro de uma certa distância, basta dividir essa distância por 3 e somar 1.
\frac{99-23}{3} = 25,3333
Como não é possível dividir o telefone, o número desejado é:
25 + 1 = 26
Alternativa correta – Letra D
Questão 64
Um comerciante vende todos os seus produtos com acréscimo de 50% sobre o valor de custo. Certo dia, ele fez uma promoção em todos os produtos que vende, concedendo desconto de 10% sobre o preço normal de venda. Nesse dia, esse comerciante vendeu cada unidade de um de seus produtos pelo preço promocional de R$ 27,00. Sendo assim, o valor unitário de custo desse produto foi
(A) R$ 22,40
(B) R$ 20,00
(C) R$ 18,60
(D) R$ 16,00
(E) R$ 14,80
Resolução
Pelo enunciado, sabemos que o preço promocional é igual ao valor unitário promocional acrescido de 50% e descontado 10%, transformando isso em equação:
P=C(1+0,5)(1-0,1)
27=C(1,5)(0,9)
C=\frac{27}{(1,5)(0,9)}
C=\frac{27}{1,35}
C=20
Alternativa correta – Letra B
Questão 65
Em uma turma com 30 alunos, sendo 13 homens e 17 mulheres, deseja-se escolher, aleatoriamente, um representante, um vice-representante e um suplente, de modo que esse grupo não seja composto somente por homens e não seja composto somente por mulheres. O número total de possibilidades para fazer essa escolha é igual a
(A) 3094
(B) 7050
(C) 10919
(D) 14786
(E) 18564
Resolução
O que iremos fazer nessa questão, é encontrar o número de possibilidades total e subtraí-lo do número de possibilidades de sair apenas homens ou apenas mulheres. O número total de possibilidades total é dado por um arranjo de 30 elementos (número de homens e mulheres) arranjados de 3 a 3.
30 \cdot 29 \cdot 28 = 24360
Enquanto que o número de possibilidades de sair apenas homens é dado por um arranjo de 13 elementos arranjados de 3 a 3.
13 \cdot 12 \cdot 11 = 1716
E mulheres, 17 elementos arranjados de 3 a 3.
17 \cdot 16 \cdot 15 = 4080
Fazendo-se as devidas operações
N = 24360 – 1716 – 4080
N = 18564
Alternativa correta – Letra E
Questão 66
Resolvendo-se a equação algébrica x^3–7x^2 + 16x = 10, identificam-se três raízes distintas. A soma dessas raízes é igual a
(A) 3
(B) 4
(C) 5
(D) 6
(E) 7
Resolução
A partir das relações de Girard, vê-se que a soma das raízes de uma equação é igual a -\frac{b}{a} onde a é o coeficiente da variável de maior grau e b o coeficiente da variável com um único grau menor que o maior. Portanto:
x_1+x_2+x_3=-\frac{-7}{1}
x_1+x_2+x_3=7
Alternativa correta – Letra E
Questão 67
O sistema linear \begin{cases} x-3y+4z = -4\\3x-7y+7z=-8\\-4x+6y-z = α-1 \end{cases} terá solução somente quando o valor de α for igual a
(A) 2
(B) 3
(C) 4
(D) 5
(E) 6
Resolução
Pelo método do escalonamento:
\left [\begin{array}{rcr} 1 & 3 & 4 & -4\\ 3 & -7 & 7 & -8 \\ -4 & 6 & -1 & {α-1} \end{array} \right]
Somando o produto da primeira e -3 à segunda linha
\left [\begin{array}{rcr} 1 & 3 & 4 & -4\\ 0 & 2 & -5 & 4 \\ -4 & 6 & -1 & {α-1} \end{array} \right]
Somando o quádruplo da primeira linha à terceira linha
\left [\begin{array}{rcr} 1 & 3 & 4 & -4\\ 0 & 2 & -5 & 4 \\ 0 & -6 & 15 & {α-17} \end{array} \right]
Somando o triplo da segunda linha à terceira linha
\left [\begin{array}{rcr} 1 & 3 & 4 & -4\\ 0 & 2 & -5 & 4 \\ 0 & 0 & 0 & {α-5} \end{array} \right]
A partir daí, podemos escrever a seguinte equação:
0x +0y+0z = α-5
0= α-5
α=5
Alternativa correta – Letra D
Questão 68
A figura apresenta um hexágono regular inscrito em uma circunferência de centro G e diâmetro igual a 20 centímetros.
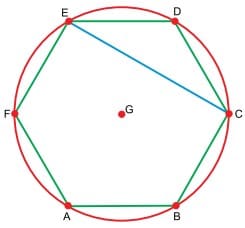
A medida, em centímetros, do segmento de reta de extremidades C e E é igual a
(A) 10\sqrt{3}
(B) 11\sqrt{3}
(C) 12\sqrt{3}
(D) 13\sqrt{3}
(E) 14\sqrt{3}
Resolução
Ao traçar uma linha do centro até os pontos E e C, percebemos que forma-se um triângulo semelhante ao triângulo EDC, logo, a distância do centro ao segmento \overline{EC} é igual a distância desse ponto até D, por isso, podemos dizer que essa distância corresponde a metade do raio.
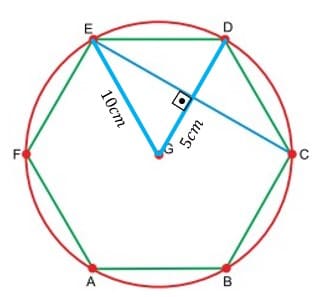
Utilizando o Teorema de Pitágoras:
d_{EC} = 2 \sqrt{10^2-5^2}
d_{EC} = 2 \sqrt{75}
d_{EC} = 2\cdot 5 \sqrt{3}
d_{EC} = 10\sqrt{3}
Alternativa correta – Letra A
Questão 69
Na igualdade a seguir, estão relacionados o tempo t, necessário para garantir um montante M, na aplicação de um capital C, à taxa de juros compostos i.
logM–logC–log(1 + i)^t = 0
Aproximando-se log 2 para 0,30 e log 3 para 0,48, uma aplicação de R$ 2.000,00, à taxa de juros compostos de 20% ao ano, gerará um montante de R$ 3.000,00 em um período de meses igual a
(A) 25
(B) 26
(C) 27
(D) 28
(E) 29
Resolução
Substituindo os valores dados no enunciado na equação, temos:
log 3000–log2000–log(1 + 0,2)^t = 0
Utilizando das propriedades do logaritmo:
log (3\cdot 1000) –log(2\cdot1000)–log(1,2)^t = 0
log (3\cdot 1000) –log(2\cdot1000)–t\cdot log(\frac{12}{10}) = 0
log 3 +log1000– (log2+log1000)–t\cdot log12 + t\cdot log10= 0
0,48 +3– (0,3+3)–t\cdot log (4 \cdot 3) + t= 0
3,48–3,3–t\cdot log 2^2 – t\cdot log3 + t= 0
0,18–t \cdot 0,6 – t \cdot 0,48 + t= 0
0,18–t \cdot 1,08+ t= 0
0,08t=0,18
t=\frac{0,18}{0.08}
t=2,25
Ou seja, 27 meses.
Alternativa correta – Letra C.
Questão 70
Na figura, os triângulos ABC e FGH são equiláteros, de lados medindo 10 centímetros.
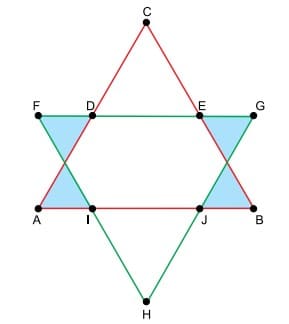
Sabendo-se que os pontos D e E dividem ao meio os lados AC e BC, respectivamente, a área, em centímetros quadrados, da região plana formada pelos quatro triângulos com o interior pintado é igual a
(A)\frac{15\sqrt{3}}{2}
(B)\frac{25\sqrt{3}}{4}
(C)5\sqrt{3}
(D)\frac{15\sqrt{3}}{4}
(E)\frac{5\sqrt{3}}{2}
Resolução
Sabendo que os dois triângulos equiláteros são idênticos, podemos dizer que os seus lados possuem a mesma inclinação, por isso, ao se cortarem, formam outros triângulos também equiláteros. Logo, todos os lados dos triângulos azuis são iguais e, sabendo que são formados a partir da metade do lado \overline{AD}, sabemos também que são iguais a 2,5cm. Usando a fórmula da área para triângulos equiláteros:
A=4\frac{l^2\sqrt{3}}{4}
A=4\frac{2,5^2\sqrt{3}}{4}
A=\frac{25\sqrt{3}}{4}
Alternativa correta – Letra B

