Questão 61
Considere um Grupamento de Policiamento Motorizado que utilize, em suas operações, dois tipos de veículos, V_1 e V_2, cujos tanques de combustível têm capacidades diferentes. Sabe-se que é possível preencher \frac{3}{4} da capacidade do tanque de V_1 , inicialmente vazio, com uma quantidade de combustível que corresponde a \frac{3}{5} da capacidade total do tanque de V_2 . A fração da capacidade do tanque de V_2 que representa a quantidade de combustível necessária para encher totalmente o tanque de V_1 é
(A) \frac{3}{20}
(B) \frac{1}{4}
(C) \frac{3}{8}
(D) \frac{2}{5}
(E) \frac{4}{5}
Resolução
O que a questão nos pede é para encontrar a parte da capacidade do tanque 2 que representa o total do tanque 1. Pelo enunciado, temos:
\frac{3}{4}V_1=\frac{3}{5}V_2
V_1=\frac{12}{15}V_2
V_1=\frac{4}{5}V_2
Alternativa correta – Letra E
Questão 62
A tabela seguinte relaciona os cinco atos infracionais mais comuns cometidos por adolescentes de 12 a 15 anos, e os respectivos números de ocorrências atendidas por policiais militares de determinado Batalhão, em certo período.
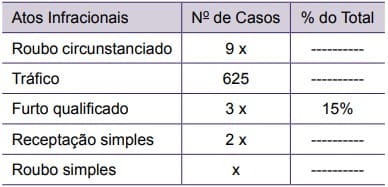
De acordo com os dados da tabela, é correto afirmar que o número de casos de roubo circunstanciado (assalto mediante ameaça com arma de fogo ou participação de duas ou mais pessoas) registrados no período considerado foi
(A) 1200
(B) 1125
(C) 1100
(D) 875
(E) 750
Resolução
Pela tabela, vemos que 3x corresponde a 15%, logo, x corresponde a 5%, além disso o somatório dos casos deve ser igual a 100%. Somando-se os números de casos, obtém-se 75% + 625, portanto, 625 casos corresponde a 25% do número total de casos, sendo assim, 125 casos correspondem a 5%.
Já que o número de casos de roubo circunstanciado é igual a 9x, ou seja, 45%, então, o número desses casos é:
N = 125 \cdot 9
N = 1.125
Alternativa correta – Letra B
Questão 63
Como treinamento, o Esquadrão Antibombas do Grupo de Ações Táticas Especiais simulou uma operação para desarmar um artefato explosivo com a utilização de um robô. Inicialmente, isolou uma região retangular MNOP em torno da suposta bomba, identificada pelo ponto B na figura, sendo B ponto médio de \overline{MO}.

Sabe-se que a região retangular, cujas medidas dos lados são proporcionais aos números 3 e 4, tem 280 m de perímetro e que o robô, guiado por controle remoto, partiu de M e dirigiu-se, em linha reta, até B. Nessas condições, é correto afirmar que a distância percorrida pelo robô nesse trajeto foi, em metros, igual a
(A) 80
(B) 75
(C) 60
(D) 55
(E) 50
Resolução
Tendo seus lados proporcionais a 4 e 3, o perímetro deve respeitar a seguinte equação, onde 3x e 4x são as possíveis medidas dos lados:
P = 3x + 4x + 3x + 4x
280 = 14x
x = \frac{280}{14}
x = 20
Logo, os lados medem 60cm, pois 3(20) = 60, e 80cm, porque 4(20) = 80.
Como o que se pede é a distância de uma das pontas até o robô, precisamos encontrar a metade da hipotenusa do triângulo retângulo formado dentro da figura.
d = \frac{\sqrt{80^2+60^2}}{2}
d = \frac{\sqrt{6.400+3.600}}{2}
d = \frac{\sqrt{10.000}}{2}
d = \frac{100}{2}
d = 50
Alternativa correta – Letra E
Questão 64
A figura seguinte mostra um reservatório com formato de paralelepípedo reto-retângulo, cujas dimensões a, b e c estão, nessa ordem, em Progressão Geométrica crescente, sendo sua soma igual a 10,5 m.
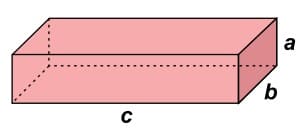
Se o volume desse reservatório é 27 m³, então a área da sua base bc é, em m², igual a
(A) 27
(B) 26
(C) 18
(D) 15
(E) 12
Resolução
O que vamos fazer é tentar tirar do enunciado o máximo de equações possíveis. Sendo uma progressão geométrica, a sequência deve estar na seguinte ordem:
a, a\cdot r, a \cdot r^2
Sendo sua soma igual a 10,5, temos:
(I)\,a + a\cdot r + a \cdot r^2 = 10,5
Além disso, o seu produto é igual a 27:
a \cdot a\cdot r \cdot a \cdot r^2 = 27
a^3r^3 = ^3
Tomando raiz cúbica em ambos os lados:
ar = 3
(II)\,a =\frac{3}{r}
Substituindo a equação (II) na (I):
\frac{3}{r} + \frac{3}{r}\cdot r + \frac{3}{r}\cdot r^2 = 10,5
Multiplicando ambos os lados da igualdade por 2r.
6 + 6r + 6r^2 = 21r
Utilizando da fórmula de bhaskara para encontrar as raízes:
r = \frac{-b\pm\sqrt{b^2-4ac}}{2a}.
r = \frac{15\pm\sqrt{225-144}}{12}.
r = \frac{15\pm\sqrt{81}}{12}.
r = \frac{15\pm9}{12}.
r_1 = \frac{15+9}{12}=2.
r_2 = \frac{15-9}{12}=\frac{1}{2}.
Voltando a (II) equação:
a=\frac{3}{2}
b=\frac{3}{2}\cdot 2 = 3
c=3\cdot 2 = 6
Portanto, o produto entre b e c é:
b \cdot c = 3 \cdot 6
b \cdot c = 18
Alternativa correta – Letra C
Questão 65
Na prova de condicionamento físico do concurso para Aluno-Oficial PM, uma das baterias da “corrida de 12 minutos” teve a participação de 9 candidatos. Admita que, nessa bateria, a média aritmética das 6 maiores distâncias percorridas tenha sido 50% superior à média aritmética das 3 menores distâncias percorridas. Nesse caso, se a média aritmética das distâncias percorridas pelos 9 candidatos foi 2,4 km, então a média aritmética das 6 maiores distâncias percorridas nessa bateria foi igual, em quilômetros, a
(A) 1,8
(B) 2,5
(C) 2,7
(D) 2,8
(E) 3,0
Resolução
Pelo enunciado, podemos tirar 2 equações.
” A média aritmética das 6 maiores distâncias percorridas tenha sido 50% superior à média aritmética das 3 menores distâncias percorridas”
M_{6+}=1,5\cdot M_{3-}
(I)\,\frac{M_{6+}}{1,5} = M_{3-}
“A média aritmética das distâncias percorridas pelos 9 candidatos foi 2,4 km”
(II)\,2,4 = \frac{a_1+a_2+…+a_9}{9}
A média dos 3 menores termos é:
M_{3-} = \frac{a_1+a_2+a_3}{3}
Logo, a soma dos três primeiros termos é:
a_1+a_2+a_3 = 3M_{3-}
Substituindo o valor de M_{3-} pela equação (I):
a_1+a_2+a_3=2M_{6+}
E a soma dos 6 últimos é:
a_4+a_5+…+a_9=6M_{6+}
Substituindo esses valores na equação (II):
2,4 = \frac{2M_{6+}+6M_{6+}}{9}
2,4 = \frac{8M_{6+}}{9}
M_{6+} = \frac{2,4 \cdot 9}{8}
M_{6+} = 2,7
Alternativa correta – Letra C
Questão 66
O número de soldados da 1ª e da 2ª Cia. de certo Batalhão eram iguais a x e y, respectivamente, sendo que a 1ª Cia. tinha 200 soldados a mais que a 2a Cia. Após um concurso, x e y foram aumentados em 5% e 10%, respectivamente, e a diferença entre o efetivo da 1ª Cia. e o da 2ª Cia. continuou a ser igual a 200 soldados. Nessas condições, é correto afirmar que, após o aumento, o número de soldados da 1ª Cia. passou a ser igual a
(A) 420
(B) 410
(C) 405
(D) 380
(E) 375
Resolução
Do enunciado, tira-se:
“a 1ª Cia. tinha 200 soldados a mais que a 2ª Cia”
x = y + 200
(I)\,y = x – 200
“x e y foram aumentados em 5% e 10%, respectivamente, e a diferença entre o efetivo da 1ª Cia. e o da 2ª Cia. continuou a ser igual a 200 soldados.”
(II)\,1,05x = 1,1y + 200
Substituindo a equação (I) na (II)
1,05x = 1,1(x – 200) + 200
1,05x = 1,1x – 220 + 200
1,1x – 1,05x = 220 – 200
0,05x = 20
x = 400
Após o aumento de 5%:
x_2 = 400\cdot 1,05
x_2 = 420
Alternativa correta – Letra A
Questão 67
Ontem, três atletas realizaram seus treinamentos percorrendo distâncias diferentes sobre uma pista circular de 300 m de diâmetro. Sabe-se que Nivaldo percorreu 2,7 km a menos que Murilo e 1,8 km a mais que Ramiro, e que, juntos, eles deram um total de 37 voltas completas nessa pista. Usando a aproximação π = 3, é correto afirmar que a distância em quilômetros percorrida por Murilo no treinamento de ontem foi
(A) 15,6
(B) 13,5
(C) 12,6
(D) 11,7
(E) 10,8.
Resolução
Sabemos que o total percorrido pelos 3 foi de 37 vezes a circunferência de diâmetro igual a 300.
N+M+R = 37\cdot 2πr
N+M+R = 37\cdot 2\cdot 3 \cdot 150m
N+M+R = 33.3 km
Sabemos também que Nivaldo percorreu 2,7 km a menos que Murilo
(I)\, N = M – 2,7km
E que Nivaldo percorreu 1,8 km a mais que Ramiro
(II)\, N = R + 1,8km
Substituindo a (I) na (II)
M – 2,7km = R + 1,8km
R = M – 4,5km
Voltando à equação principal
M – 2,7km+M+M – 4,5km = 33.3 km
3 M = 33.3 km + 4,5km + 2,7km
3 M = 40,5km
M = \frac{40,5}{3}km
M = 13,5 km
Alternativa correta – Letra B
Questão 68
Duas novas armas de longo alcance estão sendo testadas pela Polícia Militar. Sabe-se que, nas mesmas condições de tiro, a probabilidade de uma atingir exatamente o alvo é P(Q)=\frac{2}{3}, e a probabilidade de a outra atingir exatamente o alvo é P(R)=\frac{3}{4}. Sendo Q e R eventos independentes, se as duas armas disparam, a probabilidade de que ao menos um dos dois disparos atinja o alvo é de
(A) \frac{11}{12}
(B) \frac{8}{9}
(C) \frac{2}{3}
(D) \frac{1}{2}
(E) \frac{4}{9}
Resolução
A probabilidade de que ao menos um disparo atinja o alvo é igual a 100% menos a probabilidade de que nenhum atinja o alvo. A probabilidade do primeiro disparo não atingir o alvo é de \frac{1}{3}, enquanto a probabilidade do segundo disparo não atingir é de \frac{1}{4}.
P = 1 – \frac{1}{3} \cdot \frac{1}{4}
P = 1 – \frac{1}{12}
P = \frac{11}{12}
Alternativa correta – Letra A
Questão 69
Na figura seguinte, o quadrado ABCD representa o pátio de manobras de um quartel de um Regimento de Policiamento Montado, com área de 10000 m² , que foi dividido em três regiões distintas pelos segmentos \overline{EF} e \overline{EC}, sendo a região colorida de verde (gramada) reservada para treinamento dos animais.
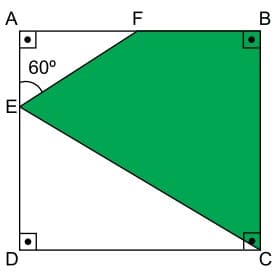
Sabendo-se que a medida do segmento corresponde \overline{EF} a \frac{2}{5} da medida do segmento \overline{AD}, e usando-se \sqrt{3} =1,7, é correto afirmar que a área, em m², da região gramada é
(A) 8300
(B) 7250
(C) 6680
(D) 5640
(E) 5450
Resolução
O que faremos é encontrar a área dos dos triângulos AEF e EDC e subtraí-las do quadrado. Sabendo que a área é de 10.000m², deduzimos que cada lado é igual a 100m.
O enunciado nos diz que o segmento \overline{AE} é igual a dois quintos do lado, ou seja, é igual a 40m. Logo, o segmento \overline{ED} é igual a 60m.
A partir dai, já podemos calcular a área do triângulo EDC.
A_{EDC} = \frac{60\cdot 100}{2}m^2
A_{EDC} = 3.000
Para a área do outro triângulo, podemos encontrar o valor do segmento \overline{AF} usando o conceito de tangente.
tg\,60º = \frac{\overline{AF}}{40}
\sqrt{3}= \frac{\overline{AF}}{40}
\overline{AF}=\sqrt{3}\cdot 40
\overline{AF}=1,7\cdot 40
\overline{AF}=68
Logo, a área do triângulo AEF é:
A_{AEF} = \frac{40\cdot 68}{2}
A_{AEF} = 1360m^2
Área verde
A_{verde} = 10.000m^2-1.360m^2-3.000m^2
A_{verde} = 5.640m^2
Questão 70
Na figura, os pontos A e B estão sobre o gráfico da função quadrática f(x) = x² – 6x + 8, e o ponto C situa-se no vértice da parábola.
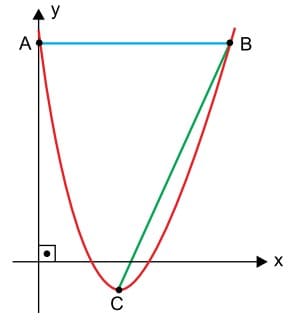
Sabendo-se que o ponto A situa-se no eixo das ordenadas e que \overline{AB} é paralelo ao eixo das abscissas, é correto afirmar que a medida de \overline{AB} é
(A)10\sqrt{3}
(B)10\sqrt{6}
(C)5\sqrt{5}
(D)3\sqrt{10}
(E)3\sqrt{5}
Resolução
O que precisamos fazer é encontrar as coordenadas dos pontos B e C.
O ponto C é o vértice da parábola, portanto, suas coordenadas são encontradas da seguinte forma:
x_v= -\frac{b}{2a}
x_v= -\frac{-6}{2}
x_v=3
Y do vértice
y_v=f(3)
y_v=3^2-6\cdot 3 + 8
y_v=-1
Logo, C(3,-1)
Sabendo que a metade de \overline{AB} é 3 e que A e B possuem a mesma coordenada em y, ou seja, 8, pois é o termo independente da função quadrática. B está situado em (6,8).
Usando a fórmula da distância entre dois pontos:
d_{C,B}=\sqrt{{(6-3)}^2+{(8+1)}^2}
d_{C,B}=\sqrt{90}
d_{C,B}=\sqrt{2 \cdot 3^2 \cdot 5}
d_{C,B}=3\sqrt{10}
Alternativa correta – Letra D

