Questão 71
“Em alguns ônibus, para cada litro de diesel comum abastecido são acrescentados 200 mililitros de biodiesel (diesel de óleos vegetais), cujo custo, por litro, é 18% maior que o do diesel comum.”
(O Estado de S. Paulo, 12.04.2014. Adaptado)
Considere os ônibus A e B, com tanques de combustíveis de capacidades iguais e inicialmente vazios, e admita que:
• No tanque do ônibus A sejam colocados 250 litros de diesel comum, e em seguida seja adicionada certa quantidade de biodiesel, na proporção indicada na notícia, enchendo-o completamente.
• O tanque do ônibus B seja totalmente preenchido somente com diesel comum.
Nessas condições, é correto afirmar que o custo do abastecimento do ônibus A terá, em relação ao do ônibus B, um acréscimo de
(A) 9%
(B) 6%
(C) 4,5%
(D) 3,6%
(E) 3%
Resolução
Sabemos pelo enunciado que para cada litro de diesel comum é colocado 200ml de biodiesel no tanque, ou seja, 20% do volume de diesel. Portanto, o tanque do ônibus A é preenchido com:
T_A = 250L_{die} + 20%\cdot 250L_{die}
T_A = 250L_{die} + 50L_{bio}
Enquanto o tanque B é preenchido com 300 L de diesel comum
A razão entre os dois valores nos dirá a diferença entre os preços.
\frac{T_A}{T_B}=\frac{250L_{die} + 50L_{bio}}{300L_{bio}}
Sabemos também que o biodiesel é 18% mais caro. Logo:
L_{bio}= 1,18L_{die}
50\cdot L_{bio}= 50 \cdot1,18L_{die}
50L_{bio}= 59L_{die}
\frac{T_A}{T_B}=\frac{250L_{die} + 59L_{die}}{300L_{bio}}
\frac{T_A}{T_B}=\frac{309L_{die}}{300L_{bio}}
\frac{T_A}{T_B}=1,03
Portanto, o acréscimo será de 3%.
Alternativa correta – Letra E
Questão 72
Na tabela, as letras q, p e m substituem as alturas, relacionadas em ordem crescente, de seis alunos do Curso de Formação de Oficiais da Polícia Militar avaliados em um exame biométrico, sendo que, nessa tabela, letras iguais correspondem a alturas iguais.
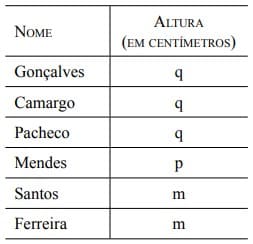
Sabendo-se que a moda, a mediana e a média aritmética das alturas desses alunos são, respectivamente, 173 cm, 174,5 cm e 175,5 cm, pode-se concluir que a altura do aluno Ferreira é igual, em centímetros, a
(A) 177
(B) 178
(C) 179
(D) 180
(E) 182
Resolução
Sabendo que a moda representa o valor dos termos que mais se repetem, q = 173.
Sendo a mediana dada, quando há um número par de termos, pela média entre os dois termos centrais quando colocados em ordem.
Mediana\, =\frac{q+p}{2}
174,5 =\frac{173 +p}{2}
p = 176
Média
Média\, = \frac{3\cdot 173 + 176 + 2m}{6}
175,5 = \frac{3\cdot 173 + 176 + 2m}{6}
6\cdot 175,5 = 3\cdot 173 + 176 + 2m
1053 = 695 + 2m
2m = 1053-695
m = \frac{358}{2}
m = 179
Alternativa correta – Letra C
Questão 73
O policiamento de um grande evento musical deteve 100 pessoas. Sabe-se que 50 pessoas foram detidas por furto de celulares, que 25 pessoas detidas são mulheres, e que 20 mulheres foram detidas por furto de celulares. Para a elaboração do relatório, o PM Jurandir montou uma tabela e inseriu esses dados, para depois completá-la.
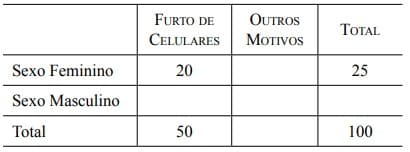
Tomando-se ao acaso uma das pessoas detidas por outros motivos, a probabilidade de que ela seja do sexo masculino é de
(A) 90%
(B) 75%
(C) 50%
(D) 45%
(E) 30%
Resolução
Preenchendo a tabela, vemos que o número de mulheres presas por outro motivos é igual a 5 e que o número de homens presos por furto de celulares foi de 30, pois o número total de pessoas presas por furto de celular foi de 50 e que 20 foram mulheres. Sabendo que ao todo 100 pessoas foram detidas, o número de homens detidos por outros motivos foi de:
H_{outros} + 20 + 30 + 5 = 100
H_{outros}= 45
A probabilidade será dada pela razão entre o valor que acabamos de encontrar e o número total de pessoas detidas por outros motivos.
P = \frac{45}{45+5}
P = \frac{45}{50}
P = 0,9
P = 90%
Questão 74
Planejando uma operação de policiamento ostensivo, um oficial desenhou em um mapa três círculos concêntricos de centro P, conforme mostrado na figura.
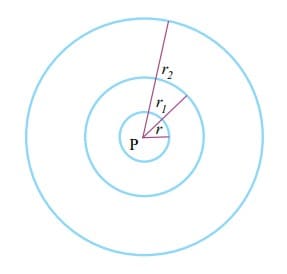
Sabe-se que as medidas dos raios r, r_1 e r_2 estão, nessa ordem, em progressão geométrica. Se r + r_1+ r_2= 52 cm, e r . r_2 = 144 cm, então r + r_2 é igual, em centímetros, a
(A) 36
(B) 38
(C) 39
(D) 40
(E) 42
Resolução
Pelo conceito de progressão geométrica, podemos escrever esses três termos da seguinte forma:
r, rq, rq^2
Pela segunda equação que nos é dada:
r\cdot r_2 = 144
r\cdot rq^2= 144
r^2q^2= 144
Tomando raiz quadrada em ambos os lados
rq= 12
r= \frac{12}{q}
r + r_1 + r_2 = 52
r + rq + rq^2 = 52
r(1+q+q^2) = 52
\frac{12}{q}(1+q+q^2) = 52
Multiplicando q em ambos os lados:
12(1+q+q^2) = 52q
12q^2 – 40q +12=0
Dividindo ambos os lados por 4:
3q^2 – 10q +3=0
Usando bhaskara para encontrar as raízes:
q = \frac{10\pm\sqrt{10^2-4(3)(3)}}{2\cdot 3}
q = \frac{10\pm\sqrt{100-36}}{6}
q = \frac{10\pm\sqrt{64}}{6}
q = \frac{10\pm8}{6}
q_1 = \frac{10+8}{6}=3
q_2 = \frac{10-8}{6}=\frac{1}{3}
Como a pg é crescente, a única raiz que nos serve é 3. Agora, basta encontrarmos r e fazermos as devidas substituições.
r =\frac{12}{q}
r =4
Equação Final
r + r_2 = r + rq^2
4 +4\cdot 3^2 = 40
Questão 75
A figura mostra um canteiro de formato circular centralizado em um jardim representado pelo quadriculado ABCD, no qual a região de cada quadradinho tem área de \frac{1}{π}m^2[\katex].
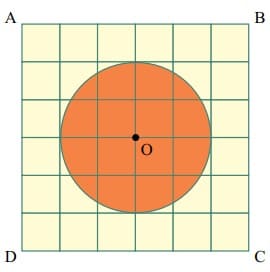
A área do canteiro de formato circular é igual, em metros quadrados, a
(A) 3,1
(B) 4
(C) 4,2
(D) 4,5
(E) 5
Resolução
Se cada quadrado possui área igual a \frac{1}{π}m^2, seu lado mede a raiz quadrada desse valor, portanto, l = \frac{1}{\sqrt{π}}m. Pela figura, vemos que o raio corresponde a dois quadrinhos, logo, o raio do círculo mede r = 2\cdot \frac{1}{\sqrt{π}}m. Pela fórmula da área do círculo, temos:
A = πr^2
A = π{(\frac{2}{\sqrt{π}})}^2
A = π\cdot \frac{4}{π}
A = 4m^2
Alternativa correta – Letra B
Questão 76
Policiais de certo batalhão foram escalados para fazer uma busca minuciosa em uma região com o formato do paralelogramo ABCD, sendo essa região dividida em duas sub-regiões por uma grande avenida, indicada na figura pelo segmento \overline{AP}.
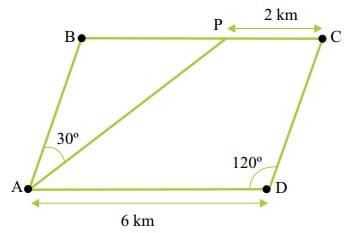
O perímetro da sub-região determinada pelo triângulo ABP é igual, em quilômetros, a
(A) 16\sqrt{2}
(B) 12\sqrt{3}
(C) 8+8\sqrt{3}
(D) 8+1\sqrt{3}
(E) 8+4\sqrt{3}
Resolução
Sabendo que a soma dos quatros ângulos internos de um paralelogramo é igual a 360º, que os ângulos opostos são congruentes e que seus lados opostos são paralelos, é possível resolver a questão. Os ângulo interno não conhecido é de 30º, como se vê abaixo:
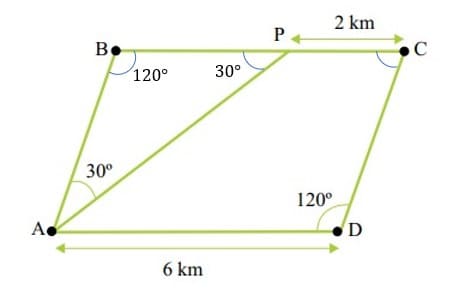
Utilizando a lei dos senos, é possível encontrar os valores dos demais lados.
\frac{sen\hat{A}}{\overline{BP}}=\frac{sen\hat{P}}{\overline{BA}}
\frac{sen30º}{4km}=\frac{sen30º}{\overline{BA}}
\overline{BA}=4km
—
\frac{sen30º}{4km}=\frac{sen120º}{\overline{AP}}
\overline{AP} = \frac{sen120º\cdot4km}{sen 30º}
\overline{AP} = \frac{\frac{\sqrt{3}}{2}\cdot4km}{\frac{1}{2}}
\overline{AP} = 4\sqrt{3}
Portanto, o perímetro do triângulo é
P = 4\sqrt{3} + 4+4
P = 4\sqrt{3} + 8
Alternativa correta – Letra E
Questão 77
A função f: R → R, dada por f(x) = ax²– 16x + c, tem um valor máximo e admite duas raízes reais e iguais. Nessas condições, e sabendo-se que c = a, é correto afirmar que o par ordenado que representa o vértice dessa parábola é
(A) (–2,0)
(B) (–1,0)
(C) (1,0)
(D) (2,0)
(E) (3,0)
Solução
Pelas relações de Girard, encontramos que a soma das raízes é igual a:
x_1 + x_2 = -\frac{b}{a}
2x = -\frac{-16}{a}
x = \frac{8}{a}
Substituindo x na equação e igualando c a a, temos:
f(x) = ax^2 -16x + c
0 = a{(\frac{8}{a})}^2 -16(\frac{8}{a}) + a
0 = a\frac{64}{a^2} -\frac{128}{a} + a
Multiplicando ambos os lados por a.
a^2 = – 64 + 128
a^2 = 64
a = \pm8
Sabendo que a função apresenta valor máximo, o valor de a é negativo, logo:
a = -8
Pela fórmula do x do vértice:
x_v = \frac{-b}{2a}
x_v = -1
Alternativa correta – Letra B
Questão 78
Em um sistema cartesiano ortogonal, observa-se um triângulo isósceles BPP’, cuja base situa-se no eixo x.
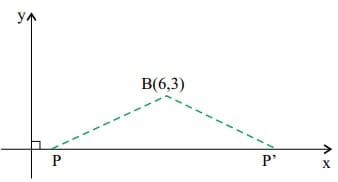
Se os pontos P e P’ distam 5 unidades de B(6,3), então a medida da base desse triângulo é igual a
(A) 12
(B) 10
(C) 8
(D) 6
(E) 4
Resolução
Dividindo o triângulo isósceles em dois triângulos retângulos, é possível encontrar o cateto que falta e consequentemente a base.
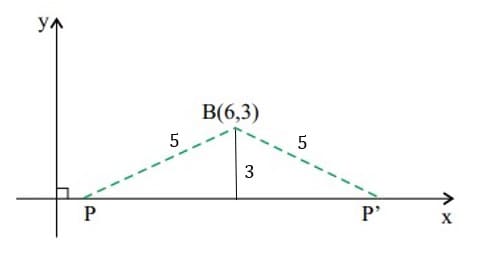
b = \sqrt{5^2-3^2}
b = \sqrt{25-9}
b = \sqrt{16}
b = 4
Logo, a base total é:
B = 2\cdot 4 = 8
Alternativa correta – Letra B
Questão 79
O novo recipiente para sabonete líquido desenvolvido por certa empresa, para ser fixado na parede, tem a forma de um prisma reto, cuja base é um triângulo equilátero de lado a:
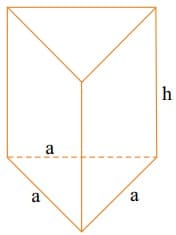
Sabe-se que a medida da altura do prisma, indicada por h na figura, é igual à medida da altura do triângulo da base. Se a = 6\sqrt{3} , então o volume dessa embalagem é igual, em centímetros cúbicos, a
(A) 324\sqrt{3}
(B) 243\sqrt{3}
(C) 216\sqrt{3}
(D) 216\sqrt{2}
(E) 162\sqrt{2}
Resolução
Sabendo que o volume da embalagem é igual ao produto entre a área da base e a altura, usaremos as seguintes fórmulas
Área da base = Área do triângulo equilátero
A_b=\frac{l^2\sqrt{3}}{4}
A_b=\frac{{(6\sqrt{3})}^2\sqrt{3}}{4}
A_b=\frac{36\cdot 3\sqrt{3}}{4}
A_b=\frac{108 \sqrt{3}}{4}
Altura da embalagem = Altura do triângulo equilátero
h=\frac{l\sqrt{3}}{2}
h=\frac{6\sqrt{3}\sqrt{3}}{2}
h=\frac{6\cdot 3}{2}
h=\frac{18}{2}
h= 9
Volume da embalagem
V = h \cdot A_b
V = 9 \cdot \frac{108\sqrt{3}}{4}
V = 243\sqrt{3}
Alternativa correta – Letra B
Questão 80
A tabela, com dados relativos à cidade de São Paulo, compara o número de veículos da frota, o número de radares e o valor total, em reais, arrecadado com multas de trânsito, relativos aos anos de 2004 e 2013:

Se o número de radares e o valor da arrecadação tivessem crescido de forma diretamente proporcional ao crescimento da frota de veículos no período considerado, então em 2013 a quantidade de radares e o valor aproximado da arrecadação, em milhões de reais (desconsiderando-se correções monetárias), seriam, respectivamente,
(A) 336 e 424
(B) 336 e 426
(C) 334 e 428
(D) 334 e 430
(E) 330 e 432
Resolução
Ao dizer que o número de radares e o valor da arrecadação são diretamente proporcionais, dizemos que eles apresentam crescimentos proporcionais ao da frota de veículos, logo, as razões entre os valores passados e futuros são iguais.
Radares
\frac{5,8}{7,5} = \frac{260}{R}
R= \frac{260 \cdot 7,5}{5,8}
R= 336
Arrecadação
\frac{5,8}{7,5} = \frac{328}{A}
A = 424
Alternativa correta – Letra A

