Há um alinhamento de três pontos quando todos eles pertencem a mesma reta, o que consequentemente a nos diz que a razão entre seus intervalos deve ser igual, o que nos indica uma mesma inclinação como veremos mais a frente, esses pontos são então chamados de colineares.
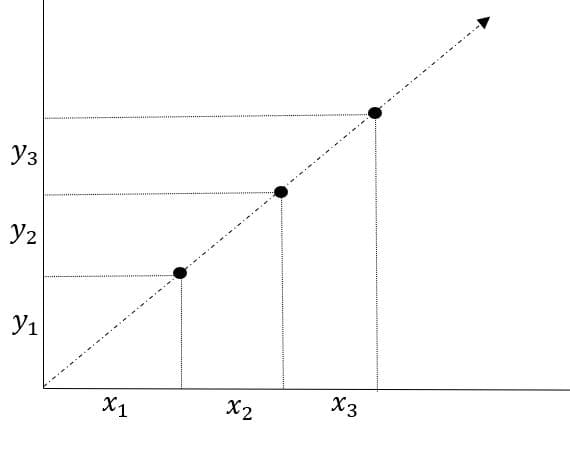
Os 3 pontos da figura pertencem a mesma reta e podemos comprovar fazendo as seguintes operações.
Basta dois pontos para que possamos formar uma reta, sendo assim, a inclinação ou taxa de variação deve ser igual para quaisquer dois pontos pertencentes a reta.
Uma outra maneira de averiguar se um terceiro ponto pode ser colinear a outros dois é escrevendo a equação da reta.
Depois de montada essa equação podemos substituir os valores de y0 e x0 pelas coordenadas de qualquer ponto da reta e então formar a equação da reta. Agora basta conferir se o terceiro ponto se encaixa.
A terceira e última maneira que trataremos nesse tópico é através do uso de matrizes.
Há uma linearidade entre essas coordenadas e podemos dizer que uma matriz formada pelas coordenadas de pontos da mesma reta, tem suas colunas proporcionais de modo que sua determinante deve ser igual a 0.
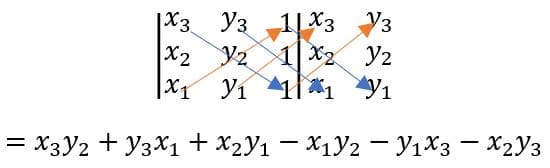
Provaremos a sentença usando a regra de Sarrus para calcular a determinante de uma matriz 3×3.
Agora através do conhecimento da equação da reta, podemos relacionar cada termo positivo a seu respectivo negativo ao dizer que:

A partir disso podemos zerar a equação.
Exemplo: Pontos da reta y = 2x
Tridimensional
O mesmo vale para um plano tridimensional, basta substituir a terceira colunas pelas coordenadas do eixo z, ou seja, o terceiro eixo, como abaixo:

FILHO, Benigno Barreto ; SILVA, Claudio Xavier. Matemática aula por aula. 2. ed. São Paulo: FTD, 2005:

