Análise Combinatória
Antes de avançarmos no estudo da análise combinatória, precisamos compreender o que significa o Princípio Fundamental da Contagem. Ele se baseia em afirmar que o número final de possibilidades para um certo acontecimento é o produto entre as possibilidades de cada etapa. Vamos a um exemplo prático!
Quantos são os gabaritos possíveis de um teste de 10 questões de múltipla escolha, com 5 alternativas por questão?
Pensemos em quantas possibilidade de reposta nós temos para cada questão.
(a) (b) (c) (d) (e)
(a) (b) (c) (d) (e)
…
Pensando apenas em duas questões, poderíamos fazer 25 marcações diferentes, pois, escolhendo uma das 5 primeiras letras para a primeira questão, teríamos também que escolher uma outra entre 5. Posto isso, as possibilidades seriam:
(a,a) (a,b) (a,c) (a,d) (a,e)
(b,a) (b,b) (b,c) (b,d) (b,e)
(c,a) (c,b) (c,c) (c,d) (c,e)
(d,a) (d,b) (d,c) (d,d) (d,e)
(e,a) (e,b) (e,c) (e,d) (e,e)
…
Seguindo esse raciocínio, podemos dizer que o número total de gabaritos diferentes, caso se marque todas as 10 questões, é de:
5 * 5 * 5 * 5 * 5 * 5 * 5 * 5 * 5 * 5 = 9.765.625
Cada abordagem que daremos ao princípio fundamental da contagem no decorrer do texto dependerá do cenário onde ele será aplicado. Ao tratar do conceito de permutação, arranjo e combinação, deixo claro que são conceitos complementares, onde cada um surge a partir de um aumento na complexidade do problema.
O exemplo acima foi retirado do livro A Matemática do Ensino Médio Volume 4. Clique aqui para conferir.
Permutação
Chamamos de permutação, a contagem que se dá excluindo um elemento até que a última possibilidade permita apenas um, ou seja, sem permitir repetições. Por exemplo, de quantas maneiras diferentes poderíamos colocar 3 pessoas em ordem em um banco de praça? Inicialmente, podemos escolher qualquer uma das 3 para ocupar o primeiro lugar, restando duas para o segundo e, por fim, apenas uma para o último. Utilizando o Princípio Fundamental da Contagem, temos:
3 * 2 * 1 = 6
Portanto, poderíamos dispor essas pessoas de 6 maneiras diferentes.
Generalizando o problema, chegamos ao conceito de fatorial, que é o produto entre todos os número iguais ou menores que um dado número. Dessa forma, podemos dizer que o fatorial representa uma permutação.
Arranjo
Como já foi discutido, cada etapa representa um aumento na complexidade do problema, sendo assim, a diferença entre um arranjo e uma permutação está no fato de que em um arranjo não usamos todos os elementos ao mesmo tempo para formar uma possibilidade. Por exemplo, tomando novamente a situação anterior, de quantas maneiras diferentes poderíamos dispor 4 pessoas em apenas 2 lugares? O primeiro lugar poderia ser ocupado por 4 pessoas, enquanto que o segundo lugar poderia ser ocupado por apenas 3. Usando o princípio:
4 * 3 = 12
Ou seja, de 12 maneiras diferentes.
Pensando no conceito de fatorial para a criação de uma fórmula genérica, podemos dizer que um arranjo é a razão entre o fatorial do número de elementos que o compõem e a diferença entre esse número e a quantidade de espaços onde eles serão alocados:
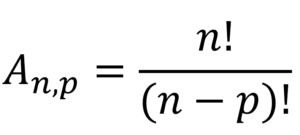
Tratemos do problema anterior a partir da fórmula.
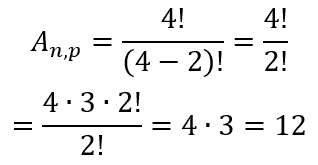
Como se Lê
Ao falar de arranjos, dizemos que existem n elementos sendo arranjados de p a p, sendo que n é sempre um número maior ou igual a p, portanto, um agrupamento de n elementos arranjados de n a n representa uma permutação
Considera-se 0! = 1
Combinação
Diferente da permutação e, consequentemente, do arranjo, na combinação não se contabiliza repetições. Por exemplo, tomando novamente a questão dada anteriormente, de quantas formas é possível agrupar 4 pessoas em 2 bancos sem que a ordem importe?
Vamos denominar essas pessoas como as seguintes letras: a, b, c, d
(a,b) – (b,a)
(a,c) – (c,a)
(a,d) – (d,a)
(c,b) – (b,c)
(c,d) – (d,c)
(b,d) – (b,d)
Existem 12 possibilidades. Deixando de considerar a ordem, considerando apenas os elementos que compõem o subgrupo, temos apenas 6 possibilidades, ou seja, o número caiu pela metade. Mas como seria se o número de lugares no banco fosse igual a 3?
(a,b,c) – (a,c,b) – (c,a,b) – (c,b,a) – (b,a,c) – (b,c,a)
Teríamos 6 possibilidades onde os mesmo elementos aparecem, portanto, ao tratar como uma combinação, teríamos apenas 1 possibilidade, ou seja, teríamos que dividir o número de combinações encontradas no arranjo por 6. O que acabamos de fazer foi encontrar uma permutação, que descreve um aspecto do nosso problema, e então dividir o número de arranjos por ela. De forma genérica, chegamos a:
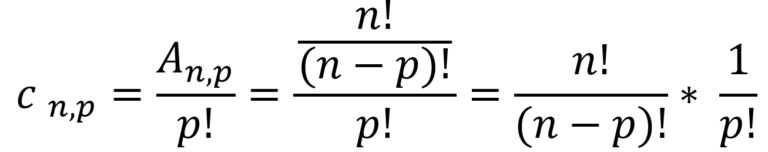
Como se Lê
Lê-se: combinações de n elementos tomados p a p. Ao analisarmos a fórmula, podemos dizer, a partir da divisão, que uma combinação representa o número de subconjuntos que possuem os mesmos elementos, já que a permutação presente no denominador indica a quantidade de elementos desses subconjuntos.
DANTE, Luiz Roberto. Matemática. 1.ed .São Paulo: Ática:2005
LIMA, Elon Lages; CARVALHO, Paulo Cezar Pinto; WAGNER, Eduardo; MORGADO, Augusto César. A Matemática do Ensino Médio: Enunciados e Soluções de Exercícios. 2. ed. Rio de Janeiro: SBM, 2016.
1 - Diagrama de Venn

