Trataremos das diferentes formas de calcular as áreas de polígonos no plano cartesiano a partir do conceito de determinante aplicado à área de triângulos, ou seja, calcularemos os demais polígonos os dividindo em triângulos.
Área de uma Região Triangular
Ao calcular a área de um triângulo em geometria plana, buscamos conhecer a base do triângulo e a sua altura. Em geometria analítica, podemos encontrar esses dados a partir das coordenadas dos três vértices. Vamos tomar como exemplo o triângulo abaixo.

Sabendo que as coordenadas dos pontos A, B e C são, respectivamente, (-7,9), (1,8) e (-3,1), podemos calcular a distância entre dois desses pontos e tomar como base do nosso triângulo. Tomaremos os pontos A e C.
Distância entre A e C
d_{AC}=\sqrt{{(-7-(-3))}^2+{(9-1)}^2}
d_{AC}=\sqrt{{(-4)}^2+8^2}
d_{AC}=\sqrt{16+64}
d_{AC}=\sqrt{80}
d_{AC}=4\sqrt{5}
Agora precisamos encontrar a altura correspondente, ou seja, o ponto do segmento \overline{AC} , ponto S, que ao ser ligado ao vértice B forma um ângulo de 90º. Para isso, precisamos encontrar a reta que possui o segmento \overline{AC} .
Reta r
m= \frac{9-1}{-7-(-3)}
m= \frac{8}{-4}
m= -2
—
(y-9) = m(x-x_0)
(y-9) = -2(x+7)
y-9 = -2x-14
y = -2x-14+9
y = -2x-5
Reta t
m= \frac{1}{2}
—
(y-8) = \frac{1}{2}(x-1)
(y-8) = \frac{x}{2}-\frac{1}{2}
y = \frac{x}{2}-\frac{1}{2}+8
y = \frac{x}{2}+\frac{15}{2}
Resolvendo o sistema formado pelas duas equações da reta a fim de encontrar o ponto S, temos:
\begin{cases} -y = \frac{x}{2}+\frac{15}{2} \\ y = -2x-5 \end{cases}
Chegamos a conclusão de que o ponto S, a intersecção entre as duas retas, tem coordenadas (5,-5). Agora, basta calcular a distância entre o ponto S e o ponto B, que é a altura do nosso triângulo.
h = \sqrt{{(8-5))}^2+{(1-(-5))}^2}
h = \sqrt{{3}^2+{6}^2}
h = \sqrt{9+36}
h = \sqrt{45}
Área do triângulo
A = \frac{4\sqrt{5}\cdot \sqrt{45}}{2}
A = 60
Áreas de Polígonos por Determinante
Através do conceito de determinante, podemos encontrar com muita mais facilidade a área de um triângulo. Posteriormente, para encontrar a área dos demais polígonos, iremos dividi-los em triângulos.
Área do triângulo
A_t = \frac{1}{2} |D|
em que D = \begin{vmatrix}x_1 & y_1 & 1 \\x_2 & y_2 & 1\\x_3 & y_3 & 1\end{vmatrix}
Calculando o valor da área do triângulo apresentado no tópico anterior através da determinante, temos:
em que D = \begin{vmatrix}-7 & 9 & 1 \\1 & 8 & 1\\-3 & 1 & 1\end{vmatrix} = 60
A_t = \frac{1}{2} |60|
A_t = 30
O mesmo resultado que encontramos a partir do método anterior.
Dividindo Polígonos
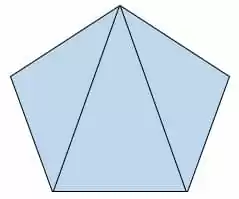
Para demonstrar como fazer a divisão dos polígonos e, só depois, calcular as áreas através do determinante, iremos calcular a área do pentágono abaixo:

As coordenadas dos pontos A, B,C,D e E são, respectivamente, (-5,0), (-8,4), (0,7), (8,4) e (5,0). Iremos dividir esse pentágono em três triângulos: ABC, ACE e CDE, onde ABC e CDE possuem a mesma área.
Área de ABC
D = \begin{vmatrix}-5 & 0 & 1 \\-8 & 4 & 1\\0 & 7 & 1\end{vmatrix} = 60
A_t = \frac{1}{2} |31|
A_t = 15,5
Logo, a área do triângulo CDE é também 15,5.
Área de CAE
D = \begin{vmatrix}-5 & 0 & 1 \\0 & 7 & 1\\5 & 0 & 1\end{vmatrix} = 60
A_t = \frac{1}{2} |70|
A_t = 35
Portanto, a área total do pentágono é:
A = 15,5+15,5+35
A = 66
O que nos permite calcular a área de polígonos, bastando apenas conhecer as coordenadas do seus vértices.
DANTE, Luiz Roberto. Matemática. 1.ed .São Paulo: Ática, 2005.

