Conhecer as formas é também conhecer o ambiente. Esse tópico irá tratar do desenvolvimento de fórmulas para o cálculo de áreas, secções e volumes, dando enfoque a cilindro, cone e esfera
Cilindro
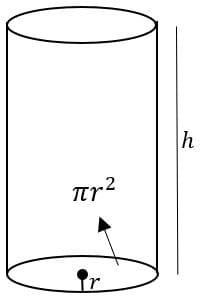
Um cilindro é formado por duas bases circulares idênticas ligadas por segmentos de reta.
O segmento que liga o centro de uma base a outra se chama eixo.
Enquanto um segmento que liga as bases a partir da circunferência é chamado geratriz do cilindro, como na figura abaixo:

Caso não tenhamos um cilindro onde o eixo é perpendicular, teremos um cilindro inclinado.
Área da Superfície
A área da superfície de um cilindro pode ser dividida em 3 partes, são elas: cada uma das bases e a região lateral.

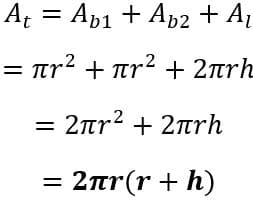
Volume
O volume de um cilindro é calculado assim como se calcula o volume de um cubo, devemos calcular a base e assim a multiplicamos pela altura, consequentemente teremos πr²*h.
Cone
Um cone é formado por uma base circular onde todos os pontos da circunferência são ligados a um único ponto fora do seu plano através de um segmento de reta.
Esse cone será reto quando quando o eixo for perpendicular a base e obliquo quando não for, ou seja, quando o cone estiver inclinado.

Área da Superfície
A superfície de um cone pode ser divida em duas partes: uma base circular e um setor circular com arco correspondente igual ao perímetro da circunferência, ou 2πr.
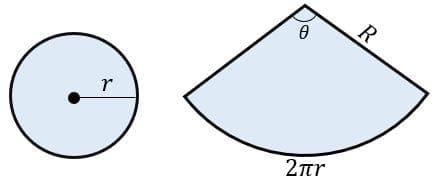
A área da base já foi apresentada, já o setor circular requer o conhecimento de novas informações.

A partir das fórmulas vemos que, a área do setor circular está para a área do circulo, assim como o comprimento do arco está para o perímetro.
Volume
O volume do cone é encontrado utilizando-se o Princípio de Cavalieri, que afirma que colocando dois sólidos sobre um plano α, ou seja, suas bases situadas no plano, e cortando-os por um plano β paralelo a α caso possuam seções de áreas iguais, então seus volumes são também iguais.
Assim, podemos associar o cone a pirâmide, chegando a conclusão que o volume do cone será:
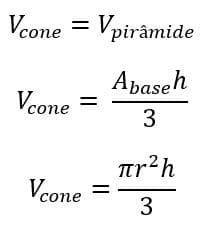
Esfera
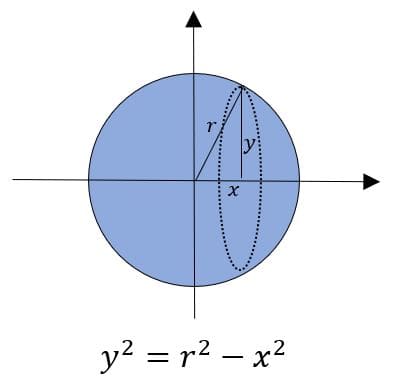
Uma esfera é um sólido formado pela rotação de um semicírculo em torno de um eixo onde está contido seu diâmetro, como na imagem abaixo:

Volume
Apresentarei primeiro o volume, pois a sua fórmula será usada para encontrarmos a área da superfícies.
Para definir o volume da esfera precisaremos de conhecimento de integrais.
Podemos entender essa integral como o somatório de todas as áreas dentro da esfera e podemos calcular a área de uma seção da esfera formando um triângulo retângulo dentro do círculo para encontrar as diversas alturas.
Agora podemos integrar a área de r a -r.
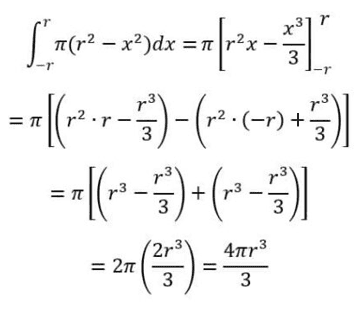
Área da Superfície
Encontraremos a área da superfície calculando a razão entre a diferença entre volumes pela diferença entre os raios, onde um é infimamente maior que o outro, ou seja, a diferença entre eles tende a 0.
Os volumes em questão serão:
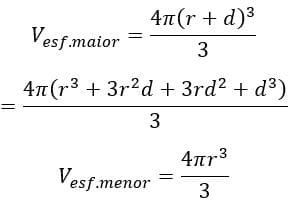
O limite que irá resultar na fórmula da superfície será:

O que acabamos de encontrar é a derivada do volume, de maneira mais simples, poderíamos calcular da seguinte forma:

STEWART, James. Cálculo. Vol. 1. 8. ed . São Paulo: Cengage Learning, 2016.
DANTE, Luiz Roberto. Matemática. 1.ed .São Paulo: Ática, 2005.
FILHO, Benigno Barreto ; SILVA, Claudio Xavier. Matemática aula por aula. 2. ed. São Paulo: FTD, 2005:

