Como Manipular Funções e Gráficos

Durante o ensino básico e médio estudamos funções do primeiro e segundo grau e seus respectivos gráficos, formamos formas a partir de pontos, traçando retas e parábolas, mas como manipular essas equações para obter os resultados desejados e como isso interfere nos seus gráficos?

Informações Sobre a Estrutura de uma função

Uma função f(x) é formada por uma parte composta por suas variáveis e seus coeficientes e por uma parte sem qualquer variável, essa última parte sozinha representa o ponto onde a função corta o eixo y.

Uma segunda informação importante é que a variável de referência pode ser manipulada, ou seja, multiplicada, dividida, somada e subtraída por um número qualquer, entenderemos agora o que cada uma dessas operações causa na equação.

Deslocamentos

Equação sem modificações:

(1) deslocar para cima:

A parte sem variável de uma equação representa a altura em que a forma irá se encontrar (f(x) = .. ax + c), ou seja, acrescentando um valor qualquer a função (f(x) = .. ax + c +b) é possível fazer ela se deslocar um número específico de casas para cima, sendo igual para qualquer valor de x.

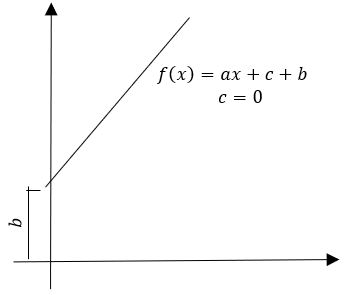
(2) deslocar para baixo:

De maneira inversa subtrair um número da função irá desloca-la casas para baixo, referente ao número que a subtraiu.

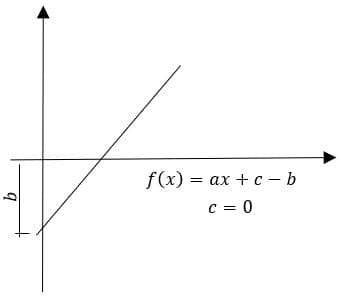
(3) Deslocar para direita:

O que determina as raízes da equação, ou seja, onde a equação corta o eixo x, são os valores pelos quais a variável x é multiplicada, para fazer a forma andar para a direita é preciso subtrair o valor da variável pelo valor a se deslocar. Exemplo para reta:

(I)\;f(x) = ax+b

(II)\; f(x-z) = a(x-z)+b

Vejamos a raiz de cada uma das equações.

(I)\;ax+b=0 \to x=\frac{-b}{a}

(II)\;a(x-z)+b \to x=\frac{-b}{a}+z

Percebe-se que a diferença de uma raiz para outra é de z, ou seja, a reta representada pela segunda equação corta o eixo x em z casas à direita em comparação a reta número (I).

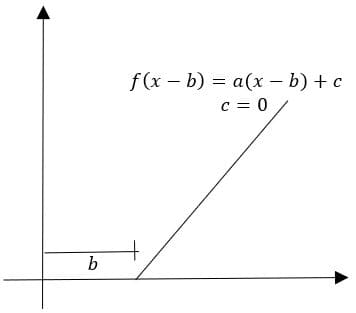
(4) Deslocar para a esquerda:

De forma análoga, para deslocar para a esquerda, é preciso somar o valor da variável pelo valor a se deslocar. Exemplo para reta:

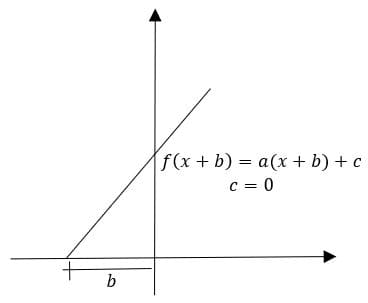
Expansões e Reflexões

A parte a qual se refere a expansão e compressão baseiam-se em princípios bem intuitivos

(5) Expandir verticalmente

É possível expandir verticalmente uma forma ao multiplicar o valor de f(x) por um coeficiente (c > 1), assim os valores de y crescem a partir desse fator multiplicativo.

(6) Comprimir Verticalmente

Já para comprimir uma forma basta dividi-la por um numero maior que 1, pois assim a função cresce ou decresce mais lentamente.

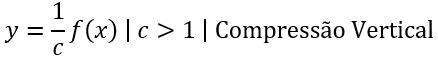
(7) Expandir Horizontalmente

Para expandir horizontalmente é preciso dividir a variável por um número maior que 1, pois assim será possível obter menores valores de y com maiores valores de x

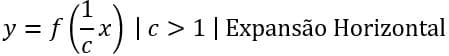
(8) Comprimir Horizontalmente

Intuitivamente, para comprimir horizontalmente, basta multiplicar a variável por um número maior que 1, pois assim será possível obter maiores valores de y com menores valores de x.