Uma dízima periódica é um número que na sua forma decimal possui infinitos números depois da vírgula, mas que, sendo um número racional, pode ser escrito em forma de fração e é isso o que vamos ver nesse tópico, como transformar dízimas periódicas em fração.
Dízimas Periódicas Simples
As dízimas periódicas são chamadas de simples quando todos os algarismos depois da vírgula se repetem, logo, todos os algarismos depois da vírgula compõe o que chamaremos de período, ou melhor, as repetições. Exemplo:
Nesse caso, o período é igual a 5.
Inicialmente, diremos que x é igual a fração correspondente ao valor da dízima, logo x = 3,555… e logo em sequência vamos manipular de uma forma que possamos tirar a dízima da equação.
1º Passo: Assumir que x é igual a dízima;
2º Passo: Multiplicar os dois lados da igualdade por uma potência de 10, cujo expoente é equivalente ao número de algarismos do período.
3º Passo: Subtrair x dos dois lados;
4º Passo: Substituir o x da direita pelo seu valor em dízima;
5º Passo: Realizar as Subtrações;
6º Passo: Isolar o valor de x.
Exemplo 1:
Aqui foi necessário multiplicar os dois lados por 10, pois há apenas um algarismo no período, que é 5, e assim encontramos que 3,555… é igual a 32/9.
Exemplo 2:
Aqui foi necessário multiplicar os dois lados por 100, ou seja, 10 elevado ao quadrado, pois, o período era formado por dois algarismos, e assim encontramos que 3,5050… é igual a 347/99.
E percebam quanto maior o período maior será o valor pelo qual deveremos multiplicar os dois lados da equação
Dízimas Periódicas Compostas
As dízimas periódicas são compostas quando há, depois da vírgula, números que não fazem parte do período, ou seja, não se repetem. Os passos para calcular a fração corresponde é semelhante a forma vista para períodos simples.
1º Passo: Assumir que x é igual a dízima;
2º Passo: Multiplicar os dois lados da igualdade por uma potência de 10, cujo expoente seja igual ao número de termos fora do período.
3º Passo: Multiplicar novamente os dois lados da igualdade por uma potência de 10, todavia, o expoente deve ser correspondente ao número de algarismos no período, gerando uma nova equação;
3º Passo: Subtrair a equação do passo 3 pela equação do passo 2.
5º Passo: Isolar o valor de x.
Exemplo:
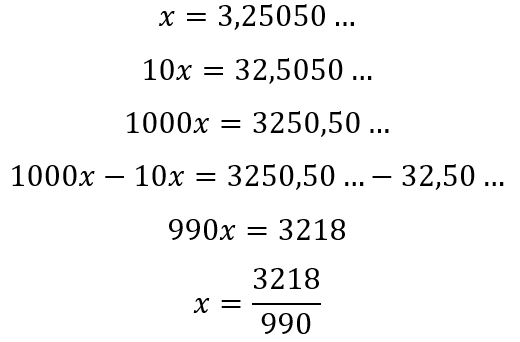
No passo 2 multiplicamos a equação por 10, pois o único algarismo fora do período era o 2 e no passo 3 multiplicamos novamente, mas, agora por 100, pois o período é formado por dois algarismo, sendo eles: 5 e 0. Encontramos que 3,25050… = 3218/990.
BARBOSA, Marco Aurélio F; JOTA, Lafayette. Matemática. Módulo 1. M1 .São Paulo: FTD, 2012.

