Matrizes e Eliminação Gaussiana
Uma matriz é uma maneira de organizar um conjunto de equações lineares e além disso, facilitar a visualização das operações que podem ser feitas para encontrar a solução para o sistema.
Operações Possíveis
(1) Multiplicar uma equação por uma constante diferente de 0.
Ao multiplicar os dois lados da equação por um certo número, a igualdade permanece válida.
(2) Inverter a posição das equações na matriz.
As equações se tocam no mesmo ponto, mudar a ordem que elas estão apresentadas não muda esse fato.
(3) É possível somar uma equação a um múltiplo de outra.
Usando a operação (1), podemos multiplicar uma equação por uma constante e depois, soma-la a uma outra equação, ou linha. Mas por que isso é possível?
Porque ao somar as taxas de variação e o valor do deslocamento em y, cria-se uma equação que interseta as demais no mesmo ponto.
Eliminação Gaussiana
O método da eliminação baseia-se em usar as operações vistas acima para chegar a linhas que relacionem uma única variável a seu respectivo valor, transformando a matriz inicial em uma matriz escalonada.
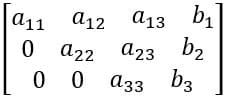
Exemplo:
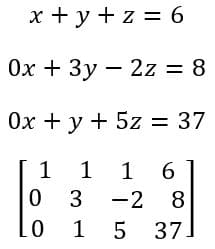
Percebam que a matriz acima não está escalonada, mas com poucas operações é possível transforma-la.
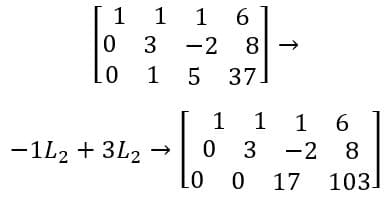
Agora, a partir da ultima linha é possível encontrar o valor da variável x3, para assim substitui-la na segunda linha e assim sucessivamente, sendo assim:



Ou seja, a solução do sistema é:
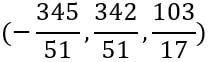
ANTON, Howard; RORRES, Chris. Álgebra Linear com Aplicações. 10. ed. Rio Grande do Sul: Bookman,2010.
KOLMAN, Bernard; HILL, David Ross. Introdução a Álgebra Linear Com Aplicações. 8. ed. Rio de Janeiro: LTC,2018.
LEON, S. J. .Álgebra Linear Com Aplicações. 9. ed. Rio de Janeiro: LTC, 2018.
