Operações Básicas com Números Complexos
O último conjunto descoberto na matemática, o conjunto dos números complexos, que engloba todos os demais conjuntos conhecidos.
Seu surgimento se deu a partir da constatação de que em certo ponto do processo para encontramos as raízes de uma equação cúbica sem o coeficiente que acompanha x², nós deveríamos inevitavelmente lidar com raízes quadradas de números negativos, gerando, a partir delas, números reais.
Foi então que em 1777, Euler criou a unidade imaginária e que mais a frente teria uma série de aplicações práticas.
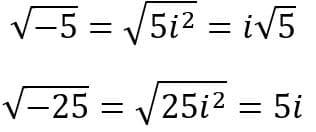
Classificações
Um número complexo é definido como um par ordenado (a, b) = a + ib = z. a representa a parte real do número e b representa a parte imaginária ou seja:
o par ordenado (a,0), representa o número real a
o par ordenado (a, b) representa o número complexo a + bi
(0,b) representa o número complexo puro bi.
Aviso: Todo número real é também um número complexo
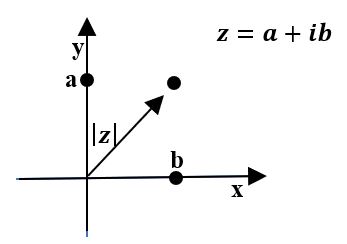
Plano Complexo ou Plano Argand-Gauss
Sendo formados por um par ordenado, os números complexos são simbolizados em um plano cartesiano específico, o plano Argand-Gauss, onde a parte real está representada pelo eixo das abscissas(x) e a parte imaginária pelo eixo das ordenadas(y)
Operações
Adição
As partes reais e as partes imaginárias são somadas separadamente:
Subtração
As partes reais e as partes imaginárias são subtraídas separadamente:
Multiplicação
A multiplicação é feita de forma distributiva, ou seja, devemos multiplicar as partes separadamente, resultado em quatros valores.
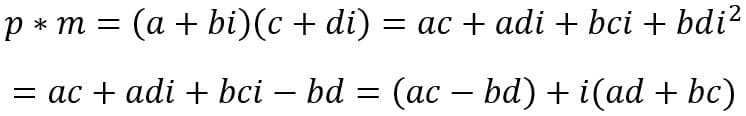
Divisão
Inicialmente devemos tirar a parte imaginária do denominador e para isso é necessário saber o conceito de conjugado, que é um numero que possui a parte real idêntica e a imaginária contraria:
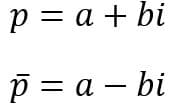
O segundo passo é multiplicar o numerador e o denominador pelo conjugado do denominador, pois assim é possível tirar a parte imaginária, assim como acontece no processo de racionalização para retirar uma raiz do denominador.
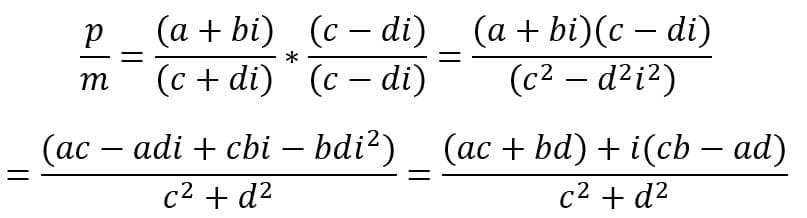
Vale lembrarmos que todas as operações acima gozam das propriedades comutativa, associativa e distributiva.
Valores de i⁰, i¹, i², i³..
A partir da definição de i, sabemos que o aumento no valor do expoente em números naturais retorna valores cíclicos, então basta apenas dividirmos os valores
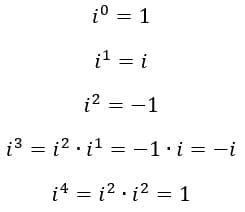
Consequentemente, basta que dividamos expoentes maiores que três, por quatro, a partir do resto podemos dizer qual o valor correspondente. Por exemplo, supondo que temos i elevado a 41, o resto é 1, ou seja, esse valor é igual a i.
BROW, James; CHURCHILL, Ruel. Variáveis Complexas e Aplicações. 9. ed. São Paulo: AMGH, 2015.
DANTE, Luiz Roberto. Matemática. 1.ed .São Paulo: Ática:2005
MOLTER, A; NACHTIGALL, C; ZHAN, M. Trigonometria e Números Complexos. São Paulo: Blucher, 2020.
