Conjuntos
Os conjuntos surgiram a partir da necessidade de exprimir propriedades e condições, evitando grandes textos e facilitando operações.
Sendo assim, dizer que “um número x possui uma propriedade N” e dizer que “y cumpri a condição M” é igual a x ∈ A, sendo A o conjunto dos números que possuem a propriedade N, e x ∈ B, sendo B o conjunto dos números que cumprem a condição M.
Operações com Conjuntos
União e Interseção
A união de dois conjuntos é expressa pelo termo ( ∪ ), ou seja, A∪B engloba todos os termos presentes no conjunto A e B, consequentemente, ao dizer que x ∈ A∪B, dizemos que ele necessariamente pertence a algum dos dois conjuntos, ou seja, pertence a A ou pertence a B.
Aviso: diferente do modo que é usado cotidianamente, esse “ou” também engloba a possibilidade de pertencer a A e B simultaneamente.
Exemplos:

A interseção de dois conjuntos é expressa pelo termo ( ∩ ), ou seja, A∩B engloba os termos que coincidem nos conjuntos A e B, consequentemente, ao dizer que x ∈ A∩B, dizemos que ele necessariamente pertence a A e B simultaneamente.
Exemplos:

Propriedades das Operações
As operações com conjuntos são comutativas, ou seja, independem da ordem em que a união ou interseção se dá, ou seja:
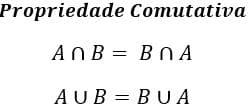
Associativas. É possível dividir todo o processo em pequenas operações, sendo o resultado sempre o mesmo, ou seja:

Distributivas. A união ou interseção de um conjunto A, pela interseção ou união de um conjunto B e C é igual a uma distribuição onde A se relaciona separadamente com os dois conjuntos, ou seja:

Operações e a Relação de Inclusão
Existem algumas associações que podem ser feitas a partir das relações entre as operações e a inclusão, sendo elas:
Ou seja, em um caso como o apresentado, todos os números que existem em A, também existem em B, portanto a união é igual a B – ou um termo pertence a A ou a B – seguindo esse raciocínio, podemos dizer que A está contido em B, e que a interseção é igual a A, pois todos os termos que coincidem se encontram em A.
LIMA, Elon Lages. Matemática do Ensino Médio. Vol. 1. Rio de Janeiro: SBM, 2016.
