Realizar operações com vetores se baseia em compreender a sua forma algébrica e como ela se dá no plano. O que veremos aqui será somente as propriedades da soma e da multiplicação aplicadas ao conceito de vetores.
Caso ainda não conheça o conceito de combinação linear e, consequentemente, não conheça o tratamento algébrico de vetores. Clique aqui.
Igualdade de Vetores
Dois vetores \vec v=(x_1,y_1, z_1) e \vec p=(x_2,y_2, z_2) são iguais se e somente se
x_1 = x_2, y_1 = y_2 e z_1 = z_2
Exemplos
Nas figuras abaixo, vemos dois vetores iguais que começam em pontos diferentes.
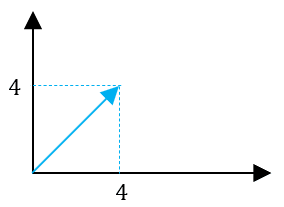
\vec v = (4-0, 4-0)
\vec v = (4, 4)
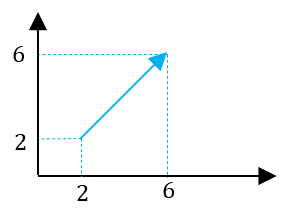
\vec p = (6-2, 6-2)
\vec p = (4,4)
Questão 1 – Determine o valor de x,y e z para que os vetores \vec t = (x-8, 13, z) e \vec m= (20, z, y) sejam iguais.
Resolução
Eixo x
x-8=20
x=20 + 8
x=28
Eixo y
13=z
Eixo z
z=y
y = 3
A partir dessa resolução, vimos que para que dois vetores sejam iguais, os vetores que os formam através de uma combinação linear também devem ser iguais.
Soma e Subtração de Vetores
Iremos primeiro analisar cada vetor separadamente no plano e, só depois, como eles se comportam quando unidos.


Se pensarmos que esses dois vetores começam na origem do plano cartesiano, o par ordenado que marcaria a distância entre a origem e o ponto final seria:
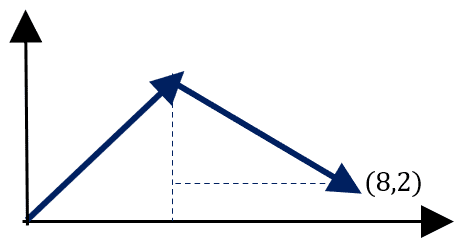
Após a soma dos dois vetores, chega-se ao ponto (8,2). O que houve aqui foi a soma algébrica de dois vetores.
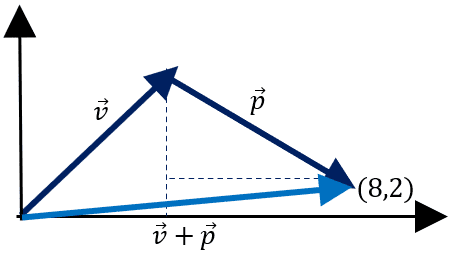
Calculando cada vetor separadamente, temos:
\vec v = 4\vec i + 5\vec j = (4,5)
\vec p=4\vec i -3\vec j = (4,-3)
Somando-se abscissa com abscissa e ordenada com ordenada:
\vec v + \vec p=(4+4)\vec i +(5-3)\vec j = 8\vec i +2\vec j
\vec v + \vec p= (4+4, 5-3) = (8,2)
Caso fosse uma subtração, teríamos:
\vec v-\vec p=(4-4)\vec i +(5-(-3))\vec j = 8\vec j
\vec v-\vec p= (4-4, 5-(-3)) = (0,8)
Veríamos da seguinte forma no plano:

Como já foi discutido, a soma de vetores apresenta as propriedades habituais da soma, então:
Propriedades
(1) \vec p + 0= \vec p
(2) \vec p + \vec v= \vec v + \vec p
(x_1,y_1) + (x_2,y_2)= (x_1+x_2,y_1+y_2)
(x_2,y_2)+(x_1,y_1) = (x_2+x_1,y_1+y_2)
(3) \vec p + (\vec{-p})= 0
\vec v + (\vec{-v})= (x_1-x_1,y_1,y_1) = (0,0)
(4) (\vec p + \vec v)+\vec m = \vec p + (\vec v+\vec m)
Ao multiplicar um vetor por um escalar, iremos encontrar um vetor cujos componentes correspondem ao produto dos componentes anteriores e um dado número, ou seja:
\vec p = (x,y)
n\vec p = (nx, yx)
Mas vejamos na prática.
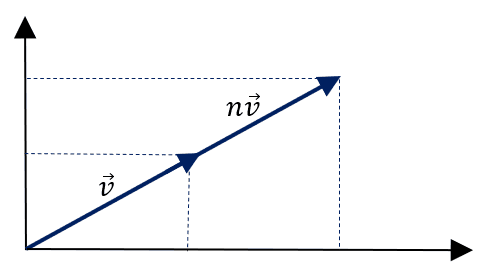
O que temos aqui é nada mais que somas e subtrações de vetores que possuem a mesma direção e que serão escritos na forma de um único vetor, por exemplo, ao somar \vec v + \vec v, temos a soma de dois vetores de mesmo módulo, mesma direção e mesmo sentido, cujo resultado é 2\vec v. Na seguinte subtração \vec v-\frac{\vec v}{2}= \vec v(1-\frac{1}{2})=\frac{1}{2}\vec v fazemos operações com vetores de mesma direção. De forma mais detalhada:
Exemplo 1
(1) 2\vec v = \vec v+\vec v = (x,y)+(x,y) = (2x,2y)
Exemplo 2
(2) \frac{1}{2}\vec v = \vec v-\frac{1}{2}\vec v
Assim como o que acontece na soma, a multiplicação também respeitas as regras já conhecidas.
Propriedades
(1) 1\vec p = \vec p
(2) a(b\vec p) = b(a\vec p)
(3) (a+b)\vec p = a\vec p + b\vec p
(4) a(\vec p+\vec v) = a\vec p+a\vec v
WINTERLE, Paulo. Geometria Analítica. 2. ed. São Paulo: Pearson Education do Brasil, 2014.
SANTOS, Fabiano José dos; FERREIRA, Silvimar Fábio. Geometria Analítica. Porto Alegre: Bookman, 2009.

