Esse tópico ira tratar de espaços amostrais equiprováveis, ou seja, onde todos os seus elementos tem a mesma chance de acontecer.
Não sabe o que é um espaço amostral ou um evento? Clique aqui.
Seguiremos com os cálculos e interpretações desse espaço e dos eventos possíveis dentro dele.
Probabilidade de Acontecer
Imaginemos que uma pessoa tira uma carta de um baralho comum que contém 53 cartas. Seu espaço amostral é dado por todas as cartas do baralho, ou seja:
Ω = {rei de copas, rainha de espadas,…)
Agora pensemos, qual a probabilidade dessa pessoa tirar o rei de copas?
O evento onde a pessoa tira o rei de copas é
A = {rei de copas}
que consta apenas um elemento.
Então, a chance de tirar o rei de copas é uma dentre 53.
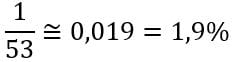
Dividindo o evento pelo espaço amostral chegamos a probabilidade desse evento acontecer. Há uma probabilidade de 1,9% de retirar exatamente o rei de copas do baralho.
De maneira genérica, temos:

P(A) irá ser sempre maior ou igual a 0 ou menor ou igual a 1.
Caso P(A) seja igual a 0, dizemos que A é um evento impossível, ou seja, não há probabilidade de acontecer.
Caso P(A) seja igual a 1, dizemos que é um evento certo, ou seja, tem 100% de chance de acontecer e para isso é preciso que o número de elementos do evento seja igual ao número de elementos do espaço amostral (todas as possibilidades).
Probabilidade de Não Acontecer
A probabilidade de um evento não acontecer corresponde a razão de todos os elementos que não pertencem a ele pelo espaço amostral. Esse conjunto que possui os elementos não pertencentes a A se chama complementar de A em relação a Ω, e o chamaremos de B.
Consequentemente, a razão dada pela soma do conjunto A mais o conjunto B pelo espaço amostral é igual a 1, pois:
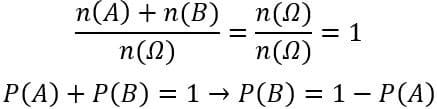
Em outras palavras, a chance de um evento não acontecer é simplesmente 100% menos a chance dele acontecer. Por exemplo, ao jogar um dado, a probabilidade dele cair em um número específico é de aproximadamente 17%, consequentemente a probabilidade de não cair nele é de 83%.
RIBEIRO, Jackson. Matemática: ciência, linguagem e tecnologia, 2. São Paulo: Scipione, 2010.

