Probabilidade e conjuntos são temas que estão infimamente relacionados. Quanto falamos de espaço amostral e evento, estamos falando de conjuntos.
Não sabe o que é um espaço amostral ou um evento? Clique aqui.
Ainda não entende como encontrar a probabilidadede de um vento acontencer ou de não acontecer? Clique aqui.
União de Eventos
Ao tratarmos de probabilidade, muito comumente nos deparamos com um número alto de eventos e precisamos calcular as chances deles em relação aos outros, para isso é necessário somar esses eventos, ou seja, os conjuntos que indicam o número de possibilidades.
Exemplos:
Você é dono de uma loja e vende dois tipos de produto, produto A e produto B. Para saber como seguir com seus investimentos, faz uma pesquisa para saber qual produto seus clientes preferem e quais as probabilidades de um deles querer o produto A, o produto B ou ambos, nisso são entrevistadas 200 pessoas.
Preferem o produto A – 50
Preferem o produto B – 75
Preferem ambos – 25
O espaço amostral do nosso problema contém 200 elementos, ou 200 pessoas, ou seja:
O evento A contém 50 pessoas e o evento B contém 75.
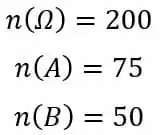
Para encontrar a probabilidade de um cliente preferir o produto A, basta calcular a razão entre n(A) e n(Ω). O mesmo vale para o produto B.
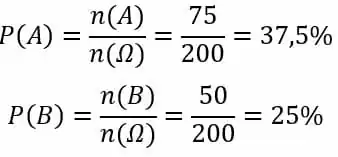
Já para encontrar a probabilidade dele querer um dos dois, precisamos encontrar o número de elementos correspondente aos elementos da união entre A e B. Percebam que o número de elementos da união não é igual a soma do número de elementos dos eventos, salvo o caso onde a intersecção é igual a 0.
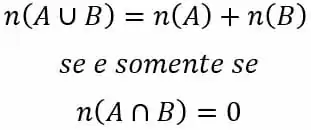
Isso é verdade, pois nesse caso não existirão elementos repetidos. Caso existam itens repetidos teremos que acrescentar a lado direito da igualdade (-(A∩B)), pois assim estaremos tirando do resultado as repetições de elementos.
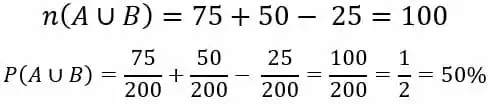
Percebemos então que a probabilidade de um novo cliente escolher um dos dois produtos é de 50%.
Probabilidade Condicional
O conceito de probabilidade condicional está associado a intersecção de conjuntos, ou seja, encontramos a probabilidade de um evento onde os elementos pertencem simultaneamente a dois ou mais conjuntos, em relação ao todo ou a conjuntos específicos.
Tomando o exemplo anterior, qual a probabilidade de um cliente querer ao mesmo tempo os dois produtos?
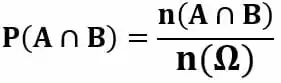
Essa probabilidade será dada pela fórmula acima, ou seja, a probabilidade de um cliente querer os dois produtos é a intersecção entre os conjuntos daqueles que escolhem o produto A e daqueles que escolhem o produto B dividido pelo número de clientes total. Temos então:
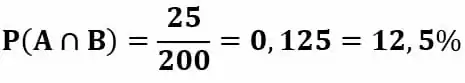
A probabilidade é então de 12,5%.
E se precisássemos saber a probabilidade de um dos clientes que escolheram o produto A também escolher o produto B? Então teríamos:
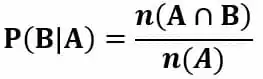
O que será chamado de probabilidade condicional de B em relação a A.
Para o nosso exemplo temos:
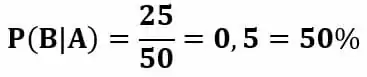
Concluímos que a probabilidade de um dos clientes que preferem o produto A gostar também do produto B é de 50%.
RIBEIRO, Jackson. Matemática: ciência, linguagem e tecnologia, 2. São Paulo: Scipione, 2010.

