O conjugado de um número complexo z = (a,b) = a + bi é:
O conjugado é descrito pela mesma letra, todavia, com um traço acima.
Sendo assim, vamos aos exemplos:
se z=5+5i, então \bar{z}=5-5i
se z=-5-5i, então \bar{z}=-5+5i
Percebam, a única parte que é alterada é a parte imaginária, que é multiplicada por -1.
se z=i, então \bar{z}=-i
se z=5, então \bar{z}=5
Concluímos que um número complexo é igual a seu conjugado apenas se a parte imaginária for igual a zero.
Um número complexo é um par ordenado, logo, podemos ver, geometricamente, os números acima e seus conjugados da seguinte forma:
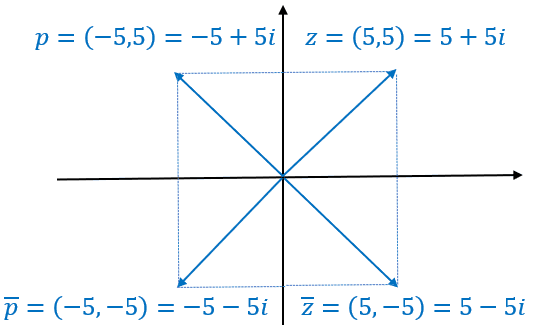
Propriedades do Conjugado
1º Propriedade: O produto de um número complexo pelo seu conjugado é igual a soma do quadrado da parte real a e o quadrado da parte imaginária b.
2º Propriedade: O conjugado da soma é igual a soma dos conjugados.
3º Propriedade: O conjugado do produto é igual ao produto dos conjugados.
Vemos também o conceito de conjugado no processo de racionalização, que é o processo no qual tornamos um denominador irracional em um denominador racional e isso apenas multiplicando o denominador e o numerador pelo conjugado do denominador.
Assim como na racionalização, o conceito de conjugado irá nos auxiliar no processo de divisão, como veremos abaixo:
Ao multiplicar o numerador e o denominador pelo conjugado do denominador, podemos resolver a divisão gerando valores satisfatórios.
DANTE, Luiz Roberto. Matemática: contexto e aplicações. 1. ed. 3 vol. São Paulo: Ática, 2010.
GÓES, Anderson Roges Teixeira; GÓES, Heliza Golaço. Números Complexos e Equações Algébricas. Curitiba: InterSaberes, 2015.

