Qual a Área das Regiões Destacadas?
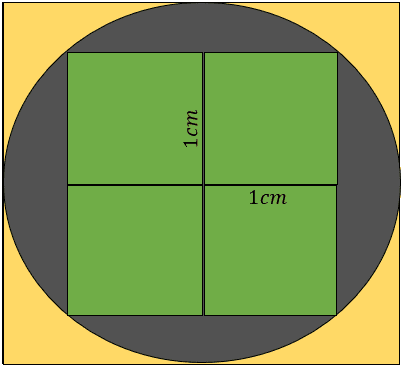
Nesse problema, vamos encontrar a área da região verde, cinza e amarela, relacionando e subtraindo formas. Inicialmente, vemos que a área verde é um quadrado formado por 4 quadrados menores, onde cada um possui lado igual a 1cm.
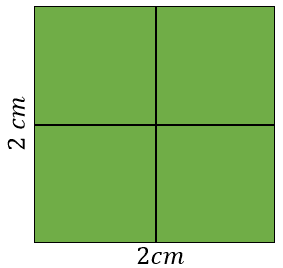
A área do quadrado é igual ao seu lado elevado ao quadrado, logo, 2 cm * 2 cm = 4 cm²
Agora, vamos a área da círculo. O diâmetro do círculo é igual a diagonal do quadrado maior, pois, como podemos observar na imagem abaixo, a diagonal do quadrado corta o centro do círculo e liga duas extremidades.
E o raio é igual a diagonal do quadrado menor, pois, partindo do centro, vai até a extremidade.
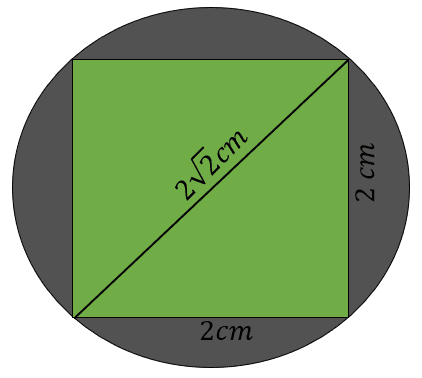
A área cinza é igual a área do círculo de diâmetro 2√2cm subtraída a área do quadrado de lado 2 cm.
A área do círculo é πr² = π(√2cm)² = 2π cm², logo, a área cinza é 2π cm² – 4 cm² ≅ 2,283 cm².
A última área, a amarela, é igual a área do quadrado, que é maior que o círculo, menos a área do círculo. O lado do quadrado é igual ao diâmetro do círculo, pois, o diâmetro do círculo pode ser encontrado traçando-se um segmento de reta que é paralelo ao lado do quadrado e que liga os dois lados da forma.
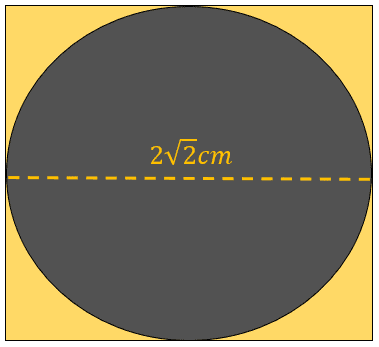
Vemos, a partir da imagem acima, que a área amarela é igual a área do quadrado de lado 2√2cm, menos a área da circulo.
A = ( 2√2cm * 2√2cm ) – 2π cm² = 8 cm² – 2π cm² ≅ 1,717 cm².
Encontramos, a partir de simples associações, todas as áreas.

