Relações Entre Retas
Existem relações que comumente usamos para classificar as retas, e que nos dão uma visão da sua estrutura no plano, e além disso tornam a linguagem mais simples e prática. Podemos relacionar as retas quanto as suas inclinações, pontos em comum e ângulos formados.
Retas Concorrentes
Retas concorrentes são aquelas que pertencem ao mesmo plano, ou seja, são coplanares, e se tocam em apenas um ponto, consequentemente possuem inclinações diferentes.
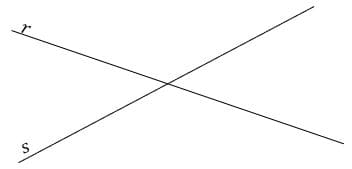
Oblíquas
Retas obliquas são aquelas que sendo coplanares, se tocam em um ponto, formando ãngulos diferentes de 90º.

Perpendiculares
Retas perpendiculares são aquelas que sendo coplanares, se tocam em um ponto, formando ângulos de 90º.
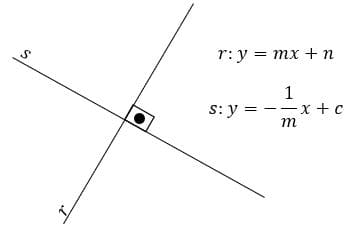
Percebe-se que para uma reta ser perpendicular a outra, ela deve ter sua inclinação igual ao inverso do contrário da outra, como mostra as fórmulas. Por outro olhar, o produto das inclinações deve ser igual a -1. Mas, por quê?

Se traçarmos uma linha ligando a reta r e reta s, como o que acontece na figura, e analisarmos os triângulos formados, podemos dizer que b por c é igual a c por a, por relações de triângulos. Multiplicando os dois lados por (-a/c) temos que o produto das inclinações é igual a -1.
Temos que b por c é a inclinação da reta r, que é razão entre os valores de y e x, em outras palavras, altura e comprimento, já a por c é a inclinação da reta s, que é negativa porque é decrescente.
Retas Paralelas
Duas retas são paralelas quando possuem a mesma inclinação e cortam o eixo y em pontos diferentes, pois isso garante que elas não se tocam em nenhum ponto.
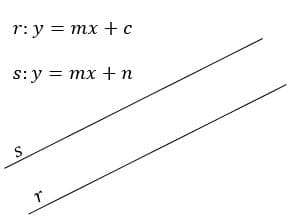
O que percebemos das retas paralelas é que as duas apresentam o mesmo valor de inclinação, ou seja, a tangente dos ângulo formados com os eixos são iguais para as duas retas.
AXLER, Sheldon. PRÉ-CÁLCULO: Uma Preparação para o Cálculo. 2. ed .Rio de Janeiro: LTC, 2016.
