Trigonometria no Triângulo Retângulo
Um triângulo é retângulo quando um dos seus ângulos é reto, ou seja, possui 90º. Triângulos são vistos normalmente no nosso dia a dia em pontes, detalhes de casas, brinquedos, instrumentos e etc., entretanto nem apenas coisas matérias são representadas por triângulos, eles também representam coisas abstratas.
Por exemplo, um veiculo uniformemente acelerado tem sua velocidade crescendo igualmente a cada instante, se temos uma linearidade, temos então uma reta, que posta no eixo cartesiano pode formar um triângulo retângulo, a área desse triângulo é, nesse caso, a velocidade média do corpo.
Teorema de Pitágoras
O teorema de Pitágoras irá nos trazer informações importantes para o entendimento dos triângulos. Afirma que o quadrado da hipotenusa(lado maior) é igual a soma dos quadrados dos catetos(lados menores):
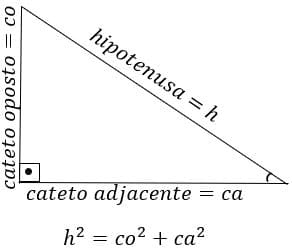
A classificação dos catetos depende da posição de referência do ângulo.
Proporções
Existem três relações entre os lados de um triângulo que serão fundamentais para desenvolver quaisquer outras relações, são elas: seno, cosseno e tangente.
Seno
O seno é a razão entre o lado oposto ao ângulo e a hipotenusa e cresce proporcionalmente a altura, então tem valor mínimo em 0 e 180º , pois a altura é zero, e tem seu módulo máximo a 90º e 270º, pois esses ângulos se encontram exatamente no eixo y. Seus valores variam de 0 a 1, pois o cateto oposto pode ir de 0 até um valor igual a hipotenusa.
Cosseno
O cosseno é a razão entre o lado adjacente ao ângulo e a hipotenusa e cresce proporcionalmente ao comprimento, então tem valor mínimo em 90º e 270º , pois seu valor no eixo x é zero, e tem seu módulo máximo a 0º e 180º, pois esses ângulos se encontram exatamente no eixo x. Seus valores variam de 0 a 1.
Tangente
A tangente é a razão entre o lado oposto e o lado adjacente ao ângulo e cresce proporcionalmente a altura e inversamente ao comprimento. Tem seu valor mínimo coincidindo com o do seno, ou seja, em 0º e 180º. Diferente das outras relações, a tangente não tem ponto máximo, pois a medida que o cosseno tende a 0, a tangente tende ao infinito, pois o seno seria dividido por um número cada vez menor.
Relações entre Seno, Cosseno e Tangente
Existem um conjunto de relações que irão facilitar o cálculo de senos, cossenos e tangentes mais complicadas ou que não apresentam alguma certa variável.
(a) Relação Fundamental do Triângulo Retângulo
sen^2 α+cos^2 α = 1, 0º < α < 90º
Demonstração:
(b) Se dois ângulos são complementares, então a soma de dois ângulos α e β é igual a 90º, consequentemente o sen α = cos β e tg α = 1/tg β.
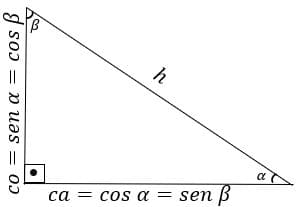
Na figura, enquanto o cateto é adjacente a α é ao mesmo tempo oposto a β, com isso podemos dizer que o cosseno α é igual ao seno de β.
Essa é igualdade é verdadeira pois o cateto oposto de um é o cateto adjacente do outro, ou seja, as tangentes são inversas.
(c) Se 0 < α < 45º, então sen 2α = 2(senα)(cosα)
A sua demonstração é feita encontrando a área de um triangulo isóceles de duas maneiras diferentes, onde uma leva em consideração o sen 2α para encontrar um dos lados.
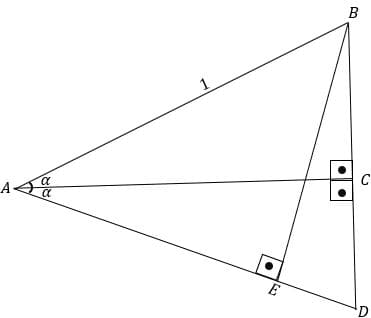
Em um dos triângulos é usado AC como altura, já no outro, EB.
Enquanto BE = sen 2α, BD = 2sen α

Ângulos Mais Recorrentes (30º,45º,60º)
Começaremos pelo ângulo de 45º, pois os ângulos de 30º e 60º partem do mesmo princípio.
Ângulo de 45º
Para que haja um ângulo de 45º é preciso ter uma base igual a altura, para que esse triângulo retângulo seja metade de um quadrado. Pelo teorema de Pitágoras temos:

Ângulo de 30º e 60º
Os dois são encontrados tomando um triangulo equilátero e dividindo-o em dois triângulos retângulos.
Como todos os ângulos são iguais, então cada ângulo mede 60º, dividindo o triângulo em dois, um deles acaba por ser duas parcelas de 30º.
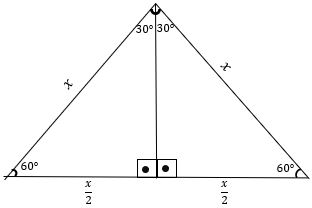
Através do Teorema de Pitágoras encontramos a altura.

Agora basta relacionar os lados e encontra o seno, o cosseno e a tangente.
Para 30º:

Para 60º:

DANTE, Luiz Roberto. Matemática. 1.ed .São Paulo: Ática, 2005.
YOUNG, Cynthia Y. .Álgebra e trigonometria. 3. ed. Rio de Janeiro: LTC,2017.
