Vamos inicialmente tratar do conceito de grandezas escalares e vetoriais para que possamos compreender o conceito de vetores juntamente com a sua aplicação.
Grandezas escalares são aquelas que podem ser definidas somente por um número e uma unidade de medida, por exemplo, a nossa massa, nossa altura e a nossa temperatura, ao falar dessas grandezas informamos apenas, respectivamente, quantos quilogramas, quantos metros e quantos graus.
Grandezas vetoriais são aquelas que, além de virem definidas por um número e uma unidade, precisam de uma direção e um sentido, um exemplo é a grandeza força, pois toda força é aplicada em algum lugar e isso precisa ser definido. Ao falar de direção, estamos nos referindo a horizontal, vertical, a 30º graus em relação ao eixo das ordenadas, etc., em outras palavras, é a reta por onde passa a grandeza, enquanto ao falar de sentido, estamos falando de esquerda, direita, cima e baixo. Outros exemplos seriam a aceleração, a velocidade e o deslocamento.
Dessa forma, um vetor representa algo que pode ser medido e que possui direção e sentido.

Supondo que todos os segmentos possuem a mesma inclinação, podemos dizer que são vetores paralelos e, possuindo o mesmo tamanho, a mesma direção e o mesmo sentido, podemos dizer que esses vetores são iguais, pois eles independem do lugar de onde partem, o que determina o vetor é a diferença entre o ponto final e o ponto inicial.
Como Escrever Vetores
Podemos representar um vetor das seguintes formas:
\overrightarrow {AB} = B – A = (x_b-x_a,y_b-y_a) = \vec v
Relembrando os conceitos já apresentados, vetores que começam e terminam em pontos diferentes de A e B podem ser idênticos ao vetor acima, pois o vetor só considera o deslocamento.
Módulo de um Vetor
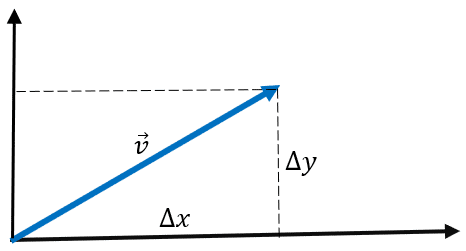
Geometricamente, sendo um vetor o deslocamento dado em cada eixo de forma separada, o seu módulo seria a hipotenusa de um triângulo retângulo de catetos iguais a \triangle x e \triangle y. A partir do teorema de Pitágoras, temos que o módulo de um vetor é igual a:
|\vec v|=\sqrt{\triangle x^2 + \triangle y^2 }
Relações Entre Vetores
Paralelos
Assim como retas paralelas, o paralelismo entre vetores é representado por duas barras:
\vec p // \vec v
Vetores paralelos apresentam a mesma direção, ou seja, a mesma inclinação, mas necessariamente apresentam o mesmo sentido. Caso apresentem a mesma direção, o mesmo sentido e o mesmo módulo, esses vetores são iguais:
\vec p = \vec v
Caso apresentem o mesmo módulo, a mesma direção, mas sentidos contrários, esses vetores são opostos:
\vec p = -\vec v
Supondo que o vetor comece e termine no mesmo ponto, a diferença entre os pontos é zero, portanto, o vetor é nulo e por não possuir direção e sentido, é considerado como paralelo a todos os demais.
Ortogonais
Vetores são ortogonais quando formam um ângulo de 90º graus entre si, ou seja, um ângulo reto, e é representado da seguinte forma:
\vec p \perp \vec v
Coplanares
Vetores são coplanares quando pertencem ao mesmo plano, ou seja, dois vetores são sempre coplanares, pois os dois juntos podem representar um plano, quando pensamos em três vetores, esse terceiro pode não ser coplanar em relação aos demais.
Imaginemos dois vetores situados no chão de uma sala, ou seja, apenas ocupam as duas dimensões que formam o chão, esses dois vetores são coplanares, pois estão situados em um plano. Agora imaginemos um terceiro vetor que vai do chão até o teto, esse terceiro vetor não é coplanar em relação aos demais, pois está fora do plano.
WINTERLE, Paulo. Geometria Analítica. 2. ed. São Paulo: Pearson Education do Brasil, 2014.
SANTOS, Fabiano José dos; FERREIRA, Silvimar Fábio. Geometria Analítica. Porto Alegre: Bookman, 2009.

