Arcos Trigonométricos
As formas costumam se relacionar entre si, e o conhecimento dessas relações facilita os cálculos e, principalmente, as interpretações. Os arcos trigonométricos e a equação da circunferência é um exemplo disso, onde o estudo de triângulos se associa a círculos. É sempre possível formar um triângulo circunscrevendo-o em um círculo, então, a partir disso, é possível igualar certas medidas. Por exemplo, ao traçar uma linha do centro ate a extremidade do círculo formaremos um triangulo retângulo em relação aos eixos.
Sendo assim, Euler desenvolveu tal fórmula:
A primeira linha é a maneira padrão de se escrever domínio e contra-domínio e quer dizer que todo número real no domínio gera um número pertencente a circunferência, ou seja, fica limitado ao raio.
A segunda linha trata dos parâmetros para calcular a distância do ponto em relação aos eixos, sendo t o ângulo formado com o eixo x.
cos t representa a distância no eixo x, pois o cateto adjacente é igual a hipotenusa multiplicada ao cosseno, e tanto o seno quanto o cosseno variam de 1 a -1, então temos um círculo de raio 1 e consequentemente, uma hipotenusa igual a 1. O mesmo se aplica ao fato de sen t representar a distância no eixo y.
Equação da Circunferência
Uma outra maneira de escrever essa correspondência é através da equação da circunferência, que é representada pelo Teorema de Pitágoras.
Forma Reduzida
Forma Geral
Percebemos que com os valores de a e b zerados temos o Teorema de Pitágoras, onde o raio representa a hipotenusa e os valores de x e y os catetos. Mas o que significam esses valores de a e b? e por que são negativos?
O valor de a representa onde está localizado o centro do circulo no eixo x e o valor de b no eixo y. Intuitivamente, f(x – a) se difere de f(x), pois a primeira vai precisa de maiores valores de x para alcançar o mesmo valor de y da segunda.
Quer entender como manipular as funções e assim entender não só o porquê desses valores de a e b terem sido colocados nessa fórmula, mas também o que outros acréscimos podem causar? Clique aqui.
Percebemos também que a única diferença entre a forma reduzida e a forma geral é que na segunda o produto notável já foi feito.
Aplicação
Imaginem que precisamos calcular a distância entre duas cidades, sabendo que possuem a mesma latitude e longitudes diferentes, como podemos calcular tendo apenas o raio da terra e essas duas informações?
Cidade x – 35º N, 50º O
Cidade y – 35º N, 95º O
R = 6.371 km
r = raio a ser encontrado
Temos que ter em mente que essa diferença de ângulo deve ser aplicada não ao raio da Terra, mas ao raio do círculo paralelo ao equador que se situa a 35ºN.
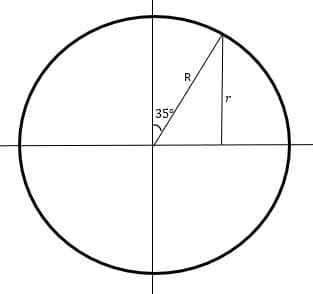
Usamos o cosseno de 35º pois ele é igual ao seno de 55º e com os dois valores é possível encontrar r.
Agora basta encontrar o arco formado pelas longitudes, lembrando, arco é uma parte da circunferência delimitada por dois ponto.
Por regra de 3 encontramos o arco e, consequentemente, a distância entre as duas cidades.
DANTE, Luiz Roberto. Matemática. 1.ed .São Paulo: Ática:2005
