O crescimento exponencial é um tipo de crescimento dado por sucessivas multiplicações, o que proporciona que os valores cresçam em quantias cada vez maiores. Para demonstrar a natureza desse crescimento, iremos abordá-lo em uma famosa história que tiro do livro O Homem que Calculava.
Lenda Sobre a Origem do Jogo de Xadrez
Em um certo período da história reinou um rei chamado Iadava, que muitos historiadores afirmam ter sido o mais rico e generoso do seu tempo. Em uma das suas varias batalhas, acabou perdendo o seu filho e entrando em profunda tristeza. Pensando em tirar o seu amado rei dessa condição que o abateu, um moço chamado Lahur Sessa trouxe ao rei um jogo de tabuleiro chamado xadrez. Não demorou para que o rei se apaixonasse pelo jogo e começasse a travar as maiores batalhas sentado com os olhos no tabuleiro e, pensando em retribuir o presente, deu ao moço a chance pedir o que quisesse. Depois de recusar a proposta, afirmando que o mais queria já tinha se cumprido, o bem do rei, foi forçado pelo rei a escolher um presente. Depois de muito pensar, Lahur pediu que lhes fossem dados grãos, todavia, contados da seguinte forma:
“Dar-me eis um grão de trigo pela primeira casa do tabuleiro; dois pela segunda, quatro pela terceira, oito pela quarta, e assim dobrando sucessivamente, até a sexagésima quarta e última casa do tabuleiro. Peço-vos, ó Rei, de acordo com a vossa magnânima oferta, que autorizeis o pagamento em grãos de trigo, e assim como indiquei!”
Diante do pedido, riram não apenas os funcionários da corte, mas também o rei. Exigiu-se dos algebristas que calculassem a quantia pedida e, após algumas horas, voltaram os calculistas com a resposta e assim afirmaram: a porção que deve ser dada a Lahur Sessa equivale a uma montanha que, tendo por base a cidade de Taligana, seria 100 vezes mais alta que o Himalaia.
Por fim, Lahur declara que abre mão do pedido e que não quis deixar o soberano aflito.
Gostaria de conferir o livro na Amazon? Clique aqui
Explicação
Esse número gigantesco é justificado pelo crescimento exponencial de grãos em relação ao número de casas do tabuleiro, vamos ao cálculo.
1 + 2 + 4 + 8 + 16 + 32 + 64 + 128 = 255
Até a 8 casa do tabuleiro, o rei precisarei ter pagado apenas 255 grãos, mas percebam a forma como esse número cresce. Já que o número sempre dobra em relação ao anterior, temos uma potência, pois essa representa uma sucessão de multiplicações, pensando assim, o número de grãos é:
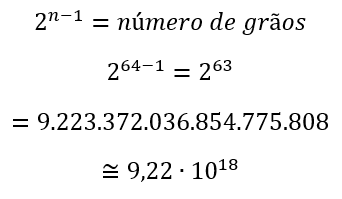
O expoente do número 2 é n – 1 pelo seguinte motivo: o valor do expoente que representa o número de grãos igual a 1, ou melhor, o número de grãos que devem ser dados na primeira casa, deve ser igual a zero, pois todo número elevado a zero é igual a 1, todavia, não existe uma casa 0, portanto, usa-se o – 1.
Funções com Crescimento Exponencial
Uma função que apresenta um crescimento exponencial tem a seguinte estrutura:
onde b deve ser um número maior do que 1, pois valores menores que 1 fariam a função se tornar decrescente, e a e k devem ser valores maiores que 0, pelo mesmo motivo.
Caso queira conhecer melhor funções exponenciais. Clique aqui
Juros Compostos
O crescimento dos juros compostos é um exemplo de crescimento exponencial, pois o juro do período seguinte é sempre dado em relação ao mês anterior. Vamos a um exemplo:
Ao colocarmos um um capital de R$2.000,00 aplicado a um juro composto de 10% ao mês, quanto teremos após 5 meses?
Mês 1: M = 2000(1+0,1) = 2200
Mês 2: M = 2020 (1+0,1) = 2420
Mês 3: M = 2040 (1+0,1) = 2662
Mês 4: M = 2662 (1+0,1) = 2928,2
Mês 5: M = 2928,2 (1+0,1) = 3221,02
Ao analisarmos os crescimentos, podemos ver que a diferença entre os valores aumenta cada vez mais.
Mês 1: 2200 – 2000 = 200
Mês 2: 2420 – 2200 = 220
Mês 3: 2662 – 2420 = 242
Mês 4: 2928,2 – 2662 = 266,2
Mês 4: 3221,02 – 2928,2 = 292,82
Generalizando, nós podemos escrever o montante, ou melhor, o capital futuro, da seguinte forma:
M = C(1 + i)ª
Onde a é o tempo. Lembrando que o tempo deve estar sempre na mesma medida que a taxa de juro.
Exercícios
(Questão 1) Qual o montante referente a aplicação de um capital de R$500,00 a uma taxa de juros compostos de 5% ao mês durante um ano e meio?
M = C(1 + i)ª
M = 500(1 + 0,05)¹⁸
M = 1203,31
Portanto, um montante de R$1.203,21.
(Questão 2) Qual deve ser o capital aplicado durante 4 meses a uma taxa de 20% ao mês a juros compostos para se obter um capital futuro de R$ 2.592,00
M = C(1 + i)ª
2.592 = C(1 + 0,2)⁴
C = 2.592/1,2⁴
C = 1250
Crescimento Populacional
O crescimento populacional é exponencial pois reconhecemos ele como um aumento que se dá periodicamente e sempre em fatores multiplicativos. Por exemplo, ao analisar uma colônia de bactérias, vemos que cada bactéria gera uma nova, portanto, de uma bactérias passam a haver duas, depois 4, depois 8, depois 16 e assim sucessivamente.
1 * 2 = 2
2 * 2 = 4
4 * 2 = 8
8 * 2 = 16
…
De maneira simples, poderíamos descrever esse problema como uma função exponencial, ou seja:
f(a) = 2ª
e se ao invés de duplicar, elas triplicassem?
1 * 3 = 3
3 * 3 = 9
9 * 3 = 27
27 * 3 = 81
…
Por consequência, a fórmula seria:
f(a) = 3ª
E se ao invés de 1 só bactéria, já começássemos com 1000 bactérias?
1.000 * 3 = 3.000 = 3 * 1.000
3.000 * 3 = 9.000 = 9 * 1.000
9.000 * 3 = 27.000 = 27 * 1.000
27000 * 3 = 81.000 = 81 * 1.000
…
Todos os resultados são multiplicados por 1000, portanto, a nossa função passa a ser:
f(a) = 1000 * 3ª
A partir desse ponto, podemos generalizar:
f(a) = p * mª
p = valor inicial
m = fator de multiplicação
t = tempo
Exercícios
(ENEM – 2016) O governo de uma cidade está preocupado com a possível epidemia de uma doença infectocontagiosa causada por bactéria. Para decidir que medidas tomar, deve calcular a velocidade de reprodução da bactéria. Em experiências laboratoriais de uma cultura bacteriana, inicialmente com 40 mil unidades, obteve-se a fórmula para a população:
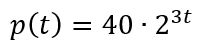
em que t é o tempo, em hora, e p(t) é a população, em milhares de bactérias. Em relação à quantidade inicial de bactérias, após 20 min, a população será:
a) reduzida a um terço
b) reduzida à metade
c) reduzida a dois terços
d) duplicada
e) triplicada.
Como já vimos, o número que multiplica o termo com expoente representa a quantidade inicial, ou seja, 40 bactérias.
Para encontrar a população de bactérias após 20min, precisamos t por esse valor, lembrando que precisamos transformar em hora, portanto t = (20/60) = 1/3, ou seja, um terço de hora.
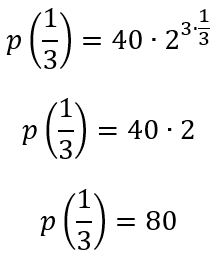
Concluímos que o número de bactérias após 20min é de 80, ou seja o número dobrou, já que passou de 40 para 80.
80/40 = 2
DANTE, Luiz Roberto. Matemática. 1.ed .São Paulo: Ática:2005
AXLER, Sheldon. PRÉ-CÁLCULO: Uma Preparação para o Cálculo. 2. ed .Rio de Janeiro: LTC, 2016.

