A equação da circunferência tem o objetivo de descrever todos os pontos pertencentes a circunferência, em outras palavras, essa equação relaciona os valores da coordenada x com os valores da coordenada y.
O que muitos não percebem ao estudar esse assunto é que equação é dada a partir do teorema de Pitágoras.
Teorema de Pitágoras na Circunferência
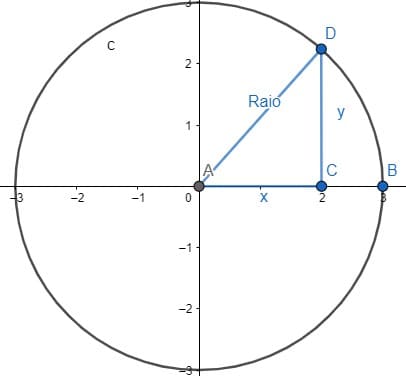
Ao olharmos o triângulo retângulo formado ligando-se o centro do círculo á sua circunferência, percebemos duas coisas sobre o triângulo.
(1) A hipotenusa do triângulo é igual ao raio do círculo.
(2) Os dois catetos do triângulo correspondem as coordenadas do ponto em x e y.
Usando o teorema, temos:
Coordenada x
Coordenada y
Circunferência com Centro fora da Origem
O trabalho desse tópico consiste em encontrar os novos valores para os catetos do triângulo retângulo, vamos deduzi-los através do gráfico
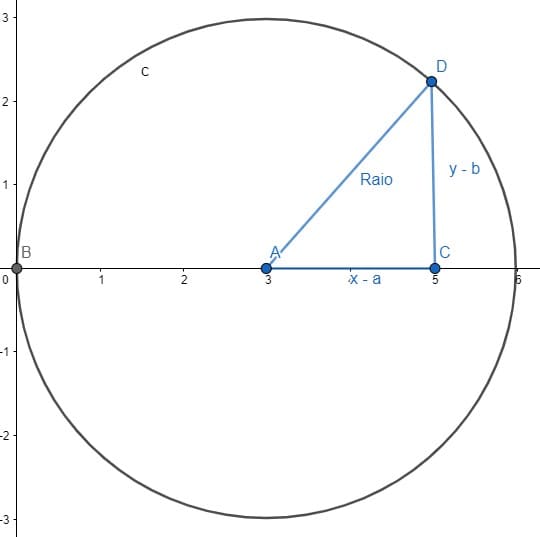
A nova circunferência se encontra a 3 unidades de distância em relação ao eixo. Pensando nisso, qual seria o valor da base do triângulo retângulo da imagem?
Ou seja, o valor da coordenada do ponto foi subtraído do valor correspondente ao centro, generalizando esse raciocínio, podemos dizer que a equação da circunferência de centro (a,b) é:
Coordenada x
Coordenada x
Equação Normal ou Geral da Circunferência
A outra maneira de escrevemos a equação da circunferência é desenvolvendo o quadrado da soma, ou seja:
Pensando na circunferência que vimos no início desse tópico, sabemos que ela possui raio igual a 3 e possui centro em (3,0), logo, a sua equação é:
E a sua equação normal é:
Percebemos que a partir da normal é muito mais complicado identificar o centro e o raio da circunferência, por isso, muitas vezes, é preciso voltar a equação original, mas como?
Método de Completar Quadrados
Utilizaremos do método de completar quadrados para chegar aos quadrados das somas.
1º passo: Separar os termos que possuem x e y
2º passo: Colocar do lado direito todos os termos que não possuem variável.
3º passo: Encontrar o termo que falta para formar o quadrado. Sabemos que o quadrado da diferença possui a seguinte estrutura:
portanto.
Partindo do termo central, temos:
Por isso, o termo que falta é 9, que é c^2.
4º passo: Somar o termo que falta em ambos os lados.
5º passo: Substituir pelo quadrado.
Exercícios de Equação da Circunferência
Questão 1) Determine a equação da circunferência cuja origem se encontra no ponto C(5,4) e que passa pelo ponto N(9,4).
Resolução
O que nos falta para montar a equação é o valor do raio. Partindo da equação genérica.
Substituindo x e y pelas coordenadas de N.
Sendo assim, a equação é:

