Lista de exercícios de progressão aritmética com questões tiradas do ENEM, vestibulares, livros e produzidas pelo próprio autor.
Querendo rever o conteúdo de progressão aritmética? Clique aqui
1º Questão – Determine o 12º termo de uma PA cuja razão é 10 e o seu primeiro termo é -20.
Resolução
Desenvolvendo esse cálculo de forma intuitiva, temos:
Utilizando a fórmula do termo geral de uma progressão aritmética
2º Questão – Determine a fórmula do termo geral de uma PA para cada sequência abaixo.
a) (1,9,16,…)
b) (5,25,45,…)
c) (x, x-y, x-2y)
Resolução
a) a_n = 1 +(9-1)(n-1)
b) a_n = 5 +(25-5)(n-1)
c) a_n = x +(x-y-x)(n-1)
3º Questão – Qual o valor do 15º número ímpar e qual a soma de todos os números ímpares iguais ou menores que ele?
Resolução
Sabemos que o primeiro termo ímpar é 1, o segundo é 3 e o terceiro é 5. A partir disso, vemos que a diferença entre eles é sempre igual a 2, em outras palavras, esses números formam uma PA de razão 2.
E usando a fórmula da soma dos termos de uma PA, temos:
4º Questão – (Enem 2ª aplicação 2014) A cada dia que passa, um aluno resolve 2 exercícios a mais do que resolveu no dia anterior. Ele completou seu 11º dia de estudo e resolveu 22 exercícios. Seu objetivo é resolver, no total, pelo menos 272 exercícios. Mantendo seu padrão de estudo, quantos dias ele ainda precisa para atingir sua meta?
a) 5
b) 6
c) 9
d) 16
e) 20
Resolução
O que a questão nos pede é que encontremos a quantidade de termos de uma PA de razão 2 que devem ser somados partindo-se do primeiro termo resultando no valor de 272. O primeiro passo será encontrar o primeiro termo conhecendo apenas o 11º.
a_1 = 22 -20 = 2[/katex
Encontrado esse valor, podemos aplicá-lo na fórmula da soma dos termos.
Dividindo toda a equação por 2, temos:
Utilizando a fórmula de bhaskara para encontrar as raízes:
Encontramos dois valores, todavia, só nos é útil o 16, pois não existe uma quantidade negativa de dias. Portanto, a alternativa correta é a letra D.
5º Questão (IF Sul Rio-Grandense 2017) – Considere uma sequência de quadrados em que o primeiro tem área 1, o segunto tem área 2 e assim sucessivamente. Sabendo que as das diagonais destes quadrados estão em progressão aritmética, a área do vigésimo quadrado em u.a., é:
a)\sqrt{40}
b)10
b)38-18\sqrt{2}
b)20
b)\frac{{(38-18\sqrt{2})}^2}{2}
Resolução
Primeiro, vamos encontrar o valor das diagonais do primeiro e segundo quadrado e, após isso, encontrar a diferença entre elas. Para encontrar o valor da diagonal, precisamos encontrar primeiro a medida do lado. Partindo do conceito de área, temos:
Quadrado 1
d_1 = 1/katex]
Quadrado 2
A partir de agora, podemos determinar a diagonal do quadrado utilizando o teorema de Pitágoras.
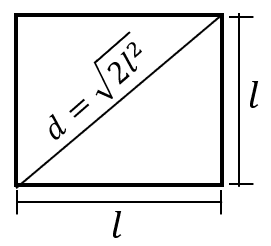
E para o segundo quadrado:
Subtraindo-os encontramos a razão da nossa PA.
Aplicando na fórmula do termo geral, encontramos a diagonal do vigésimo quadrado.
Encontrada a diagonal, iremos encontrar a área do 20º quadrado, mas para isso, encontraremos primeiro o seu lado.
Elevando ao quadrado, determinamos a área.
Portanto, a alternativa correta é a letra E.

