Definimos progressão como um desenvolvimento gradual, algo que demonstra um padrão de crescimento ou decaimento. Dessa forma. Podemos dizer que a progressão aritmética e geométrica são tipos de desenvolvimentos.
Progressão Aritmética
A progressão aritmética se dá a partir da soma sucessiva de um termo x por uma razão r , sendo crescente quando tiver sua razão positiva e negativa quando tiver sua razão negativa, formando o conjunto da progressão, como na equação:
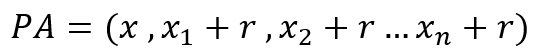
Sendo assim, a formula geral que define o termo de uma PA é dada pela formula abaixo, sendo o -1 necessário pois a contagem começa a partir do termo x1
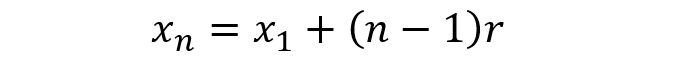
Soma dos Termos de uma Progressão Aritmética
Acredita-se que Gauss inventou a fórmula que será demonstrada em sequência aos 6 ou 7 anos de idade quando seu professor pediu a turma que respondessem qual a soma dos números de 1 a 100. O raciocínio usado para resolver se baseia no fato de que a soma do primeiro com o ultimo termo é igual a soma do segundo com o penúltimo termo ou seja 1+100 = 101 e 2+99 = 101. Intuitivamente percebe-se que existem 50 somas que resultam em 101, consequentemente, a soma dos termos da PA é 50*101 = 5050. O que resulta de maneira geral em:
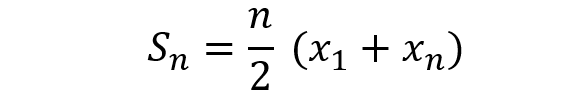
Exercícios Resolvidos
(Questão 1) Verifique se as sequências numéricas a seguir são progressões aritméticas. Sendo verdade, informar a razão.
(a) (8,13,18,23)
13 – 8 = 5
18 – 13 = 5
23 – 18 = 5
r = 5
(b) (3, 4+2x, 5+4x, 6+6x)
4 + 2x – 3 = 2x + 1
5 + 4x – 4 – 2x = 2x + 1
6 + 6x – 5 – 4x = 2x + 1
r = 2x + 1
(c) (2p – 7, 3p – 9, 4p – 11, 5p -13)
3p – 9 – 2p + 7= p – 2
4p – 11 – 3p + 9 = p – 2
5p -13 – 4p +11 = p – 2
r = p – 2
(Questão 2) Escreva os cinco primeiros termos de cada uma das progressões aritméticas a seguir sabendo que:
(a) o primeiro termo é -2 e a razão é 5.
PA = (-2, 3, 8, 13, 18)
(b) O primeiro termo é 10 e a razão é 15
PA = (10, 25, 40, 55, 70)
(Questão 3) Resolva a equação 2 + 9 + 16 + 23 + … + x = 486
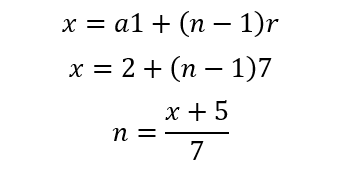
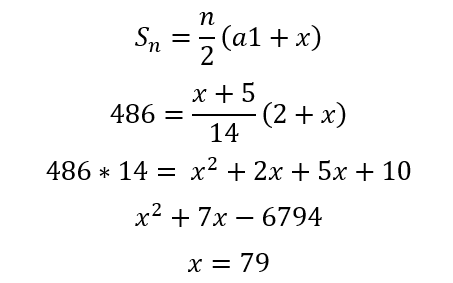
Progressão Geométrica
Uma progressão geométrica pode ser definida como uma sequência que apresenta uma taxa de crescimento relativa constante, ou seja, a porcentagem de crescimento é igual, sendo da forma:
Sendo o termo geral definido por:
Tipos de Progressões Geométricas
CRESCENTES
Podem ser crescente em duas situações:
(1) Valores positivos e razão maior que 1 ( r > 1)
(2) Valores negativos e razão maior que 0 e menor que 1 ( 0 < r <1 )
Exemplos:
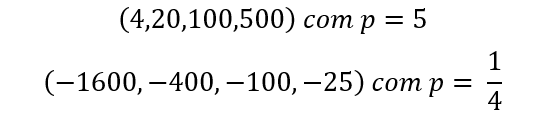
DECRESCENTES
Quando são decrescentes?
(1) Valores negativos e razão maior que 1 ( r > 1)
(2) Valores positivos e razão maior que 0 e menor que 1 ( 0 < r <1 )
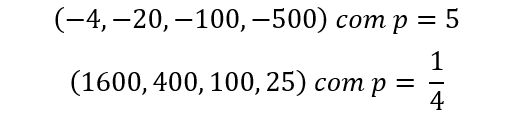
CONSTANTE
Uma progressão geométrica é constante quando a sua razão é igual a 1.
ALTERNANTE
Quando a razão é dada por um número negativo. Exemplo:
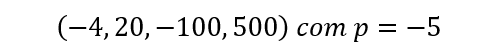
Soma dos Termos de uma Progressão Geométrica
A demonstração a seguir se deu a partir de duas considerações básicas. A primeira se refere a formula padrão da soma e a segunda, a forma padrão da soma multiplicada por q.
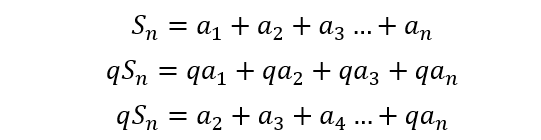
Na segunda equação, qa1 foi transformado em a2 e assim sucessivamente até o penúltimo termo, pois o último não tem correspondente na primeira equação. Subtraindo a primeira pela segunda temos:
Seguindo com as transformações e isolando Sn:
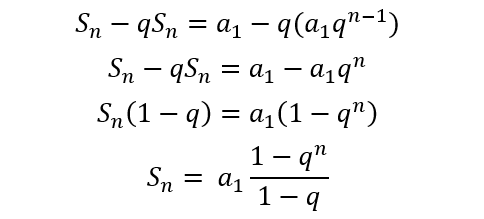
Exercícios Resolvidos
(Questão 1) Verifique se as sequências numéricas a seguir são progressões geométricas. Sendo verdade, informar a razão.
(a) (5, 40, 320, 2560)
40/5 = 8
320/40 = 8
2560/40 = 8
r = 8
(b) (5, 5x, 5x²)
5x/5 = x
5x²/5x = x
r = x
(c) (3, 3x + 3, 3x² + 6x +3)
(3x + 3)/3 = x + 1
(3x² + 6x +3)/(3x + 3) = x + 1
r = x + 1
(Questão 2) Escreva os três primeiros termos de cada uma das progressões geométricas a seguir sabendo que
(a) O segundo termo é 9 e a razão é 3
PG = (3, 9, 27)
(b) O primeiro termo é 7 e a razão é 5
PG = (7, 35, 175)
(c) O primeiro termo é 64 e a razão é 4
PG = (4, 16, 64)
DANTE, Luiz Roberto. Matemática. 1.ed .São Paulo: Ática:2005

