Observação: Alguns enunciados foram alterados em virtude da falta de disponibilidade da simbologia, todavia, a estrutura das questões se mantêm igual.
Está estudando para o Enem? Confira os assuntos da prova clicando aqui.
1º (DANTE, 2005) Examine o triângulo retângulo da figura abaixo e calcule em seu caderno o valor destas razões:
(a) sen α (b) cos α (c) tg α (d) sen β (e) cos β (f) tg β
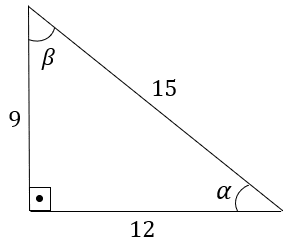
Para resolver essa questão devemos nos atentar ao significado de seno, cosseno e tangente.
seno = (cateto oposto) / (hipotenusa)
cosseno = (cateto adjacente) / (hipotenusa)
tangente = (cateto oposto) / (cateto adjacente)
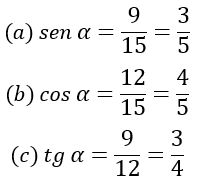
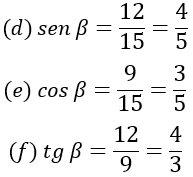
Observação: O cateto oposto é o lado oposto ao ângulo em questão.
2º (DANTE, 2005) Responda com base na análise do triângulo retângulo da figura a seguir:
(a) Qual o valor da soma α + β
(b) Indique as frações correspondentes a sen α, cos α, tg α, sen β, cos β, tg β.
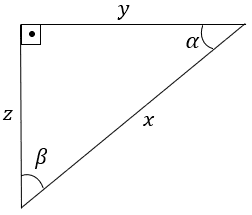
(a) A soma de todos os ângulos internos de um triângulo é igual 180º, logo, se um dos ângulos é reto, ou seja, igual a 90º, a soma dos outros dois deve ser igual, também, a 90º, pois
90º + α + β = 180º
α + β = 90º
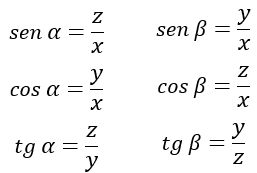
(b) Percebemos, a partir da resolução, que ângulos complementares (soma igual a 90º), possuem o seno igual ao cosseno do outro ângulo e vice-versa.
3º (DANTE, 2005) Em um triângulo EFG, retângulo em E, temos:
sen α = 5/6, cos α = (√11)/6 e tg α = (5√11)/11
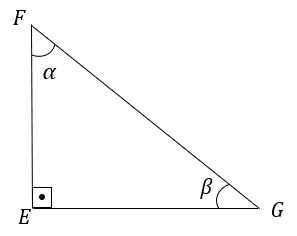
(a) Calcule sen β, cos β e tg β
(b) Se a hipotenusa do triângulo ΔEFG mede 30 cm, quanto mede os catetos?
c) Calcule o valor das expressões:
(1) (sen α)² + (cos α)²
(2) (sen α)/(cos α)
(3) sen²β + cos²β
(4) (sen β)/(cos β)
Vimos que o sen α = cos β, sen β = cos α e tg α = 1/tg β sempre que α + β = 90º, logo, a partir dessas relações, podemos resolver a letra (a)
sen β = cos α cos β = sen α
sen β = \frac{\sqrt{11}}{6} cos β = \frac{5}{6}
conhecendo o seno e o cosseno de α, podemos encontrar o seno e o cosseno de β.
Sendo a tangente de β igual ao inverso da tangente de α, basta inverter o numerador com o denominador. Ao nos depararmos com uma raiz no denominador, devemos racionalizar o número multiplicando numerador e denominador por uma raiz que nos permita deixar raízes apenas no numerador.
(b) Conhecendo a relações trigonométricas e pelo menos um lado, podemos encontrar o outros lados, vamos a resolução.
Sendo a tangente de β igual ao inverso da tangente de α, basta inverter o numerador com o denominador. Ao nos depararmos com uma raiz no denominador, devemos racionalizar o número multiplicando numerador e denominador por uma raiz que nos permita deixar raízes apenas no numerador.
c) Vamos apenas substituir os valores de seno e cosseno.
Os resultados das letras a e c são encontrados através de uma relação trigonométrica fundamental que nos diz que a soma dos quadrados de seno e cosseno de um mesmo ângulo é sempre igual a 1.
Caso ainda não conheça as relações trigonométricas fundamentais Clique aqui.
4º Encontre o perímetro do losango abaixo.
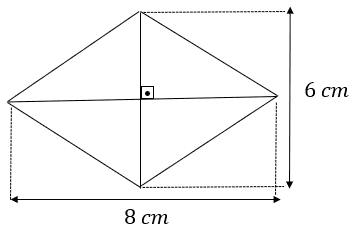
O losango é formado por 4 triângulos retângulos e suas hipotenusas representam os lados, logo, encontraremos o perímetro somando todas as hipotenusas. um dos catetos desse triângulo corresponde a metade da altura, enquanto que o outro corresponde a metade do comprimento.

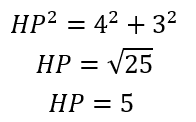
Encontramos, através do teorema de Pitágoras, o valor do lado do losango. Agora, basta somar todos os lados, ou seja, o perímetro do losango é igual a 20 = 5+5+5+5.
5º (Mack) Na figura, determine o valor de AB:

Temos conhecimento de parte do trecho AB, pois, sabemos que DC é igual a 50m, nos falta encontrar o valor do cateto oposto do triângulo retângulo. Sabemos que seno é igual a cateto oposto sobre hipotenusa, portanto:
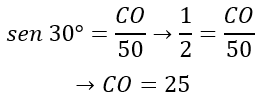
Agora, podemos calcular AB somando os trechos: 25 cm + 50 cm = 75cm = AB
O seno de 30º é um valor recorrente, por isso não houve explicação mais detalhada.
Para conhecer os valores de seno, cosseno e tangente de ângulos recorrentes Clique aqui.
6º Determine as medidas x e y nos seguintes triângulos.
a)
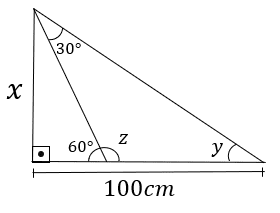
Uma das maneiras de resolver o problema é encontrar o valor do ângulo y e, após isso, utilizar o valor da sua tangente para descobrir o valor de x.
Sabemos que a soma dos ângulos internos de um triângulo é igual a 180º e podemos identificar pela imagem que os ângulos z e o de 60º graus são ângulos suplementares, ou seja, a sua soma é igual a 180º.
60º + z = 180º
z = 180º – 60º
z = 120º
Encontrando z, podemos encontrar o valor de y.
120º + 30º + y = 180º
y = 180º- 120º – 30º
y = 30º
Por fim, podemos usar o conceito de tangente para encontrar o valor de x.
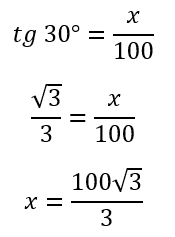
Concluímos que o valor de x é igual a (100√3)/3 cm.

