(Questão 1)(BARROSO, 2010) Uma empresa de televisão a cabo, que tem 20.000 assinantes e cobra R$35,00 mensais, fez uma pesquisa de mercado para decidir o aumento que aplicará a sua mensalidade. Os resultados desse estudo indicam que a empresa perderá 400 assinantes para cada real adicionado a mensalidade.
a) Escreva no caderno a sentença que determina o número de assinantes em função da quantidade de reais adicionados a mensalidade.
Sabemos que a empresa possui 20.000 assinantes, logo, esse é o nosso valor fixo, ou seja, o termo independente, e perderá 400 assinantes para cada real aumentado na mensalidade, portanto, a nossa sentença será uma equação do primeiro grau
b) Encontre a sentença que determina o valor de uma mensalidade, em reais, em função do aumento.
A sentença que descreve o valor da mensalidade será igual a R$35,00, valor fixo, mais o aumento.
c) Dê a lei da função que determina o faturamento mensal(em reais), dependendo da quantidade de reais adicionados na mensalidade.
O faturamento mensal é igual ao produto do número de assinantes pela mensalidade paga por cada um e todos os dois valores já foram encontrados nas duas últimas letras.
d) De quanto deve ser o aumento para maximizar o faturamento mensal?
O ponto máximo ou mínimo de uma função quadrática é chamado de vértice da parábola. O aumento máximo é então o x do vértice.
Concluímos que o aumento deve ser de R$7,50.
Caso ainda não conheça as formúlas do vértice da parábola Clique aqui.
e) Qual é a arrecadação máxima que a empresa pode obter em um mês ao aplicar esse aumento?
A arrecadação máxima é dada pelo y do vértice. Tendo o valor máximo de x, basta que a gente substitua na função.
f) Quantos assinantes deverá ter essa empresa para obter a arrecadação máxima?
O número de assinantes pode ser conseguido dividindo o faturamento máximo pelo valor pago por cada assinante.
n = 722.500/(7,5 + 35)
n = 722.500/42,5
n = 17.000
São necessários 17.000 assinantes pagando, cada um, R$42,50 para se atingir o faturamento máximo.
(Questão 2) Um livraria vende 1.000 livros por dia a R$40,00 a unidade. Percebendo que, para cada R$2,00 de desconto concedido ao cliente, o número de livros vendidos aumentava em 20 por dia.
Considerando R a receita diária total e x o desconto, em reais, concedido ao comprador. Qual a função que relaciona a receita ao desconto?
Assim como na questão 1, iremos encontrar a sentença que determina o valor unitário e a sentença que determina o número de compras.
VALOR UNITÁRIO
NÚMERO DE COMPRAS
Pois, para cada real de desconto, o número de livro vendidos aumentava em 10 por dia (esse valor pode ser encontrado através de regra de 3).
Por último, basta multiplicar as duas sentenças.
RECEITA
(Questão 3)(BARROSO, 2010) Determine o conjunto imagem das seguintes funções quadráticas:
a) f(x) = x² – 5x +1
b) g(x) = – 2x² + 3x + 7
b) h(x) = – 3x² + 8
Caso ainda não compreenda os conceitos de domínio, contradomínio e imagem de uma função. Clique aqui.
O conjunto imagem será todos os possíveis valores da função. Sendo a função quadrática descrita por uma parábola, todos os possíveis valores para f(x) = y, serão determinados pelo seu ponto máximo ou mínimo.
Letra A
Letra B
Letra C
Após encontrar os pontos máximo e mínimos de cada função, podemos determinar a imagem.
a) Im(f) = { y ∈ R | y ≥ (-21/4)}
b) Im(g) = { y ∈ R | y ≤ (65/8)}
b) Im(h) = { y ∈ R | y ≤ 8}
(Questão 4)(Enem (Libras) 2017) Suponha que para um trem trafegar de uma cidade à outra seja necessária a construção de um túnel com altura e largura iguais a 10 m. Por questões relacionadas ao tipo de solo a ser escavado, o túnel deverá ser tal que qualquer seção transversal seja o arco de uma determinada parábola, como apresentado na Figura 1. Deseja-se saber qual a equação da parábola que contém esse arco. Considere um plano cartesiano com centro no ponto médio da base da abertura do túnel, conforme Figura 2.
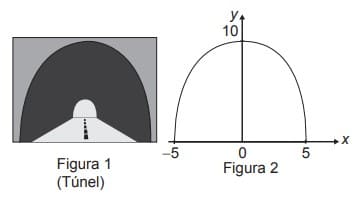
A equação que descreve a parábola é:
a) y=-\frac{2}{5}x^2+10
b) y=\frac{2}{5}x^2+10
c) y=-x^2+10
d) y=x^2-25
e) y=-x^2+25
Sabemos que a parábola corta o eixo y em 10, ou seja, o termo sem variável é igual a 10, por isso, podemos descartar a letras d e a letra e.
A concavidade está virada para baixo, portanto, o valor que acompanha x^2 é negativo, sendo assim, descartamos a letra b.
A partir do gráfico, vemos que as duas raízes da função quadrática são -5 e 5, em outras palavras, os pontos (-5,0) e (5,0) pertencem a parábola, sendo assim:
A equação que descreve a parábola é:
Letra A

