Funções Pares e Ímpares
As funções podem ser classificadas em pares e ímpares a depender da igualdade f(-x) = z e nos da informações importantes sobre a forma do gráfico, o que facilita o cálculo de formas.
Necessário:
ou seja, deve haver um número contrário a x, para que as funções possam ser classificadas como par ou ímpar.
Par
Uma função f(x) será par apenas se f(-x) = f(x). Exemplos de função pares são f(x) = cos x e f(x) = x², pois cos(-x) = cos x e (-x)² = x².
É possível identificar se uma função é par pelo seu gráfico, pois independente do valor ser positivo ou negativo ela apresenta o mesmo valor de y, ou seja, é simétrica.
Exemplo: f(x) = cos x

É possível ver pelo gráfico que cada ponto equidistante no eixo x, tem o mesmo valor de y.
Exemplo: f(x) = x²
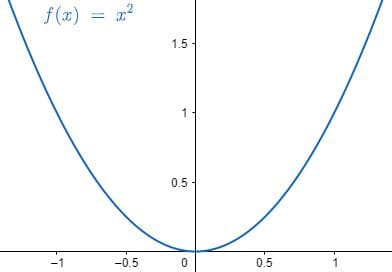
O mesmo vale para qualquer f(x) = xª , sendo a um número par.
Ímpar
Uma função f(x) será ímpar apenas se f(-x) = f(x). Exemplos de função pares são f(x) = sen x e f(x) = x, pois sen(-x) = – sen x e (-x) = -x.
Assim como para funções pares, é possível identificar se uma função é ímpar pelo seu gráfico, pois cada valor positivo de um lado do eixo y, tem um correspondente negativo do outro lado.
Exemplo: função f(x) = sen x
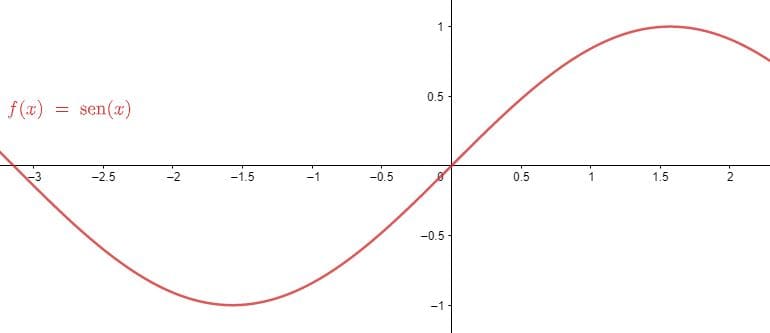
Percebemos que diferente da função cosseno, a função seno corta o eixo y em 0 e cresce pela direita e decresce pela esquerda até que atinja seu ponto máximo e mínimo.
Exemplo: função f(x) = x

O mesmo vale para qualquer f(x) = xª , sendo a um número impar. Pois todo número negativo elevado a um número ímpar resulta em outro número negativo.
Quer saber como manipular funções e seu gráficos? Clique aqui.
BARBONI, Ayrton; PAULETTE, Walter. Cálculo e Análise: Cálculo diferencial e integral a uma variável. Rio de Janeiro: LTC, 2013.
