Operações com Matrizes
Vemos operações com matrizes ao arrumar, comparar e manipular dados em linhas e colunas em um estoque, dados do IBGE e operações financeiras, além de usarmos para resolver sistemas de equações lineares, das mais simples como as que vemos na escola a sistemas gigantescos.
Conheça os principais tipos de matrizes Clique aqui.
Adição de Matrizes
Sendo uma matriz uma estrutura retangular para agrupar dados, que relaciona cada linha a uma coluna, temos que entender que para fazer a adição de duas matrizes elas precisam ter o mesmo número de linhas e colunas, para assim somar cada termo a seu correspondente.
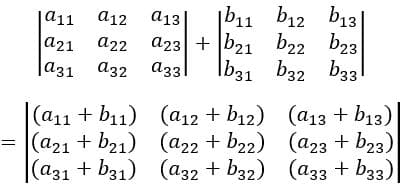
Subtração de Matrizes
A subtração se baseia na mesma ideia da subtração, cada termo de uma matriz é subtraído a seu correspondente na outra matriz.
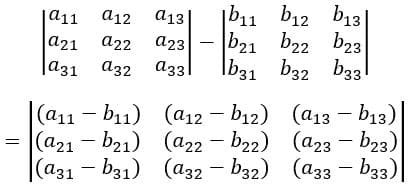
Multiplicação de Matrizes
Em comparação as outras duas operações, a multiplicação de matrizes é um pouco mais complicada, apenas porque requer que tenhamos mais atenção.
A condição para que seja possível multiplicar duas matrizes, diferente das outras operações, é que o número de colunas da primeira seja igual ao número de linhas da segunda, resultando em uma matriz com o número de linhas igual ao número de linhas da primeira matriz e o número de colunas da segunda.
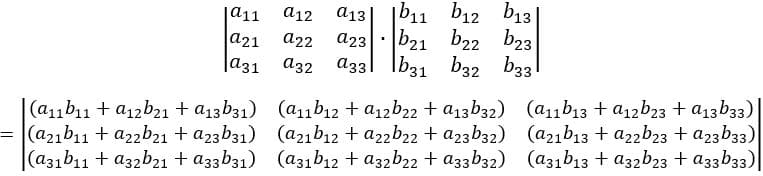
Cada linha é multiplicada por uma coluna. Percebemos a partir do desenvolvimento acima que podemos relacionar essa matriz da seguinte forma:
Análise Vertical
O primeiro elemento da matriz resultante é a soma das multiplicações da primeira linha da matriz a esquerda com a primeira coluna da segunda matriz.
O termo abaixo desse é a soma das multiplicações da segunda linha da matriz a esquerda com a primeira coluna da segunda matriz.
O enésimo termo abaixo desse é a soma das multiplicações da enésima linha da matriz a esquerda com a primeira coluna da segunda matriz.
Análise Horizontal
O primeiro elemento da matriz resultante é a soma das multiplicações da primeira linha da matriz a esquerda com a primeira coluna da segunda matriz.
O termo a direita desse é a soma das multiplicações da primeira linha da matriz a esquerda com a segunda coluna da segunda matriz.
O enésimo termo a direita desse é a soma das multiplicações da primeira linha da matriz a esquerda com a enésima coluna da segunda matriz.
Então, pensemos que sempre que fomos formar um elemento da matriz resultante, deveremos lembrar que as linha estão associadas a primeira matriz e a colunas a segunda matriz.
Multiplicação de um Número Real por uma Matriz
Ao multiplicar uma matriz por um número real, multiplicamos todos os valores que compõem essa matriz por esse número.
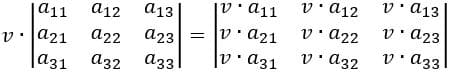
RIBEIRO, Jackson. Matemática: ciência, linguagem e tecnologia, 2. São Paulo: Scipione, 2010.
