Posições Relativas entre Reta e Circunferência
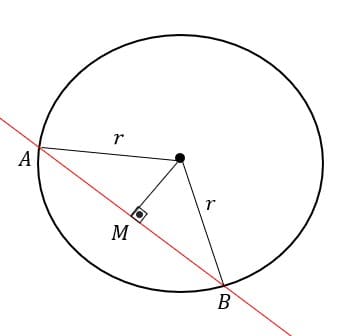
Reta Secante à Circunferência
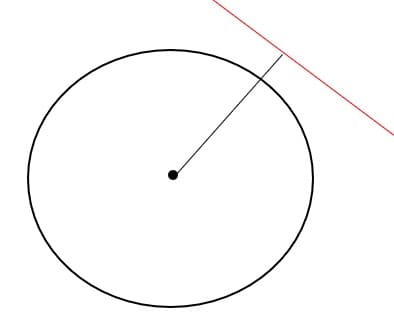
Reta Externa à Circunferência
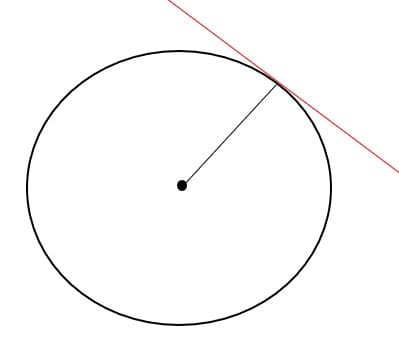
Reta Tangente à Circunferência
Como saber qual a posição da reta em relação à circunferência?
Confira antes de prosseguir:
(I,) y = -mx-n
x^2 + {(-mx-n)}^2 -2a(-mx-n)-2by +a^2+b^2-r^2=0
x^2+m^2x^2+2mxn+n^2+2amx+2an-2by+a^2+b^2-r^2=0
Assim que as devidas constantes forem estabelecidas, iremos no deparar com uma equação do segundo grau. A quantidade de pontos em que essa reta intersecta a circunferência será dada valor do discriminante (Δ=b^2-4ac) .
Δ>0 – Reta secante à circunferência. Δ=0 – Reta tangente à circunferência.Em qual ponto a reta toca a circunferência?
Os coordenadas referentes ao eixo das abscissas é encontrada através da resolução da equação do segundo grau que vimos anteriormente, em outras palavras, as raízes da equação equivalem ao valor de x dos pontos em comum entre a reta e a circunferência.
Vamos trabalhar com a circunferência de equação:
r: x^2+ y^2-2x-4y+3=0
e reta de equação:
y=2x+3
Sistema
\begin{cases}y=2x+3 \\ x^2+ y^2-2x-4y+3=0 \end{cases}
Substituindo a primeira na segunda, temos:
x^2+ {(2x+3)}^2-2x-4(2x+3)+3=0
x^2+ 4x^2+12x+9-2x-8x-12+3=0
5x^2+2x=0
Por não haver termo independente, sabemos que uma das suas raízes é zero. O que, através dos métodos usuais de resolução, nos leva a outra equação.
5x+2=0
x=-\frac{2}{5}
Agora que determinamos os valores de x, podemos substituir na nossa equação da reta a fim de encontrar as coordenadas em y.
Para x = 0
y = 2(0)+3
y = 3
Para x = -\frac{2}{5}
y = 2(-\frac{2}{5})+3
y = -\frac{4}{5}+3
y = \frac{11}{5}
Logo, os pontos onde a reta intersecta a circunferência são (0,3) e (-\frac{2}{5},\frac{11}{5})
1 - Geogebra
