Assim como a multiplicação representa a soma de elementos iguais, a potenciação representa a multiplicação de elementos iguais. Seus elementos são definidos da seguinte forma:
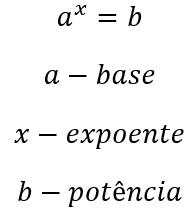
1º Propriedade da Potenciação
Em multiplicações de potências de bases iguais, somam-se os expoentes.
Como se percebe, uma segunda potência representa uma continuação das multiplicações.
2º Propriedade da Potenciação
Em divisões de potências de bases iguais, subtraem-se os expoentes.
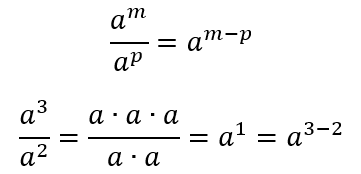
A potência que divide, ou seja, a que está no denominador, anula as multiplicações presentes no numerador. Após ler o tópico “Potência de Expoente Negativo” logo no final desse texto, peço que volte e veja essa propriedade não como uma divisão, mas como um produto.
3º Propriedade da Potenciação
A potência de uma multiplicação pode ser escrita como a multiplicação de duas potências, pois, ao contrário da potência da soma, as únicas operações que constam são multiplicações, enquanto na potência da soma constam somas e multiplicações.
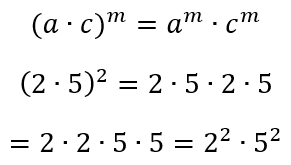
4º Propriedade da Potenciação
A potência de uma divisão pode ser escrita como a divisão de duas potências, o que já vimos na propriedade 3, já que todo número no denominador pode ser representado no número, todavia, com expoente negativo.
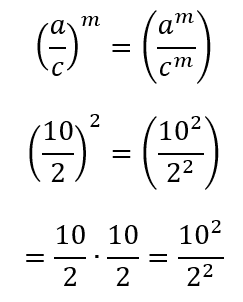
5º Propriedade da Potenciação
Em potências de potências, multiplicamos os expoentes.
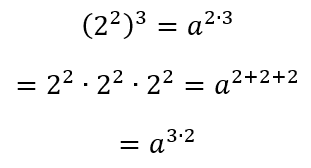
Utilizamos da 1º propriedade para provar que, elevando-se uma potência a um dado número, encontra-se o resultado somando os expoentes das potências que ele representa.
Potência de Expoente Negativo
Pensemos no fato de que todo número diferente de 0 elevado a 0 é igual a 1.
Tal fato nos permite dizer que um deve ser o inverso do outro, ou seja:
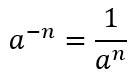
Lembrando que todas as propriedades que já foram trabalhadas se aplicam tanto a expoentes positivos quanto negativos. Vamos aos exemplos:

Exercícios Propriedades da Potenciação
(Questão 1) Calcule as potências a seguir.
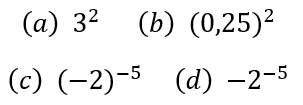
Basta que se transforme a potência em multiplicações, garantindo sempre que a base esteja em forma de fração.

(Questão 2) Aplicando as propriedades da potenciação, determine:

Todas as questões devem ser feitas seguindo os conhecimentos presentes nas propriedades, sempre se atentando ao sinal dos expoentes e as operações.

(Questão 3) Calcule usando as propriedades da potenciação.
a) x³ ⋅ x²
b) (1/2)³ ⋅ 4²
Resolução
a) x³ ⋅ x² = x⁵
b) (1/2)³ ⋅ 4² = (1/8) ⋅ 16
= 16/8 = 2
BARROSO, Juliana Matsubara. Conexões com a Matemática. 1. ed. São Paulo: Moderna, 2010
DANTE, Luiz Roberto. Matemática: contexto e aplicações. 1. ed. 3 vol. São Paulo: Ática, 2010.

