Lei dos Senos e Lei dos Cossenos
A lei dos senos e a lei dos cossenos derivam de relações já conhecidas dentro do triângulo. As duas fórmulas serão essenciais para resolver uma variedade de questões. Veremos durante o texto que cada uma será melhor aproveitada em momentos específicos, por isso, não deixaremos de trabalhar o que é necessário para usar cada uma e como aplicar isso nas questões.
Relações Trigonométricas Fundamentais
Antes de avançarmos, precisamos entender o que são as relações trigonométricas fundamentais, seno, cosseno e tangente, que são essenciais para o estudo da lei dos senos e da lei dos cossenos.
sen\,α = \frac{cateto\;oposto}{hipotenusa}
cos\,α = \frac{cateto\;adjacente}{hipotenusa}
tg\,α = \frac{cateto\;adjacente}{hipotenusa}
Essas relações que acabamos de ver, servem apenas para o triângulo retângulo e serão aplicadas para a formação da lei dos senos e da lei dos cossenos dividindo um triângulo qualquer em triângulos retângulos, como veremos mais a frente. Os valores mais usuais de seno, cosseno e tangente referem-se aos ângulos de 30º, 45º e 60º.
30º
sen 30º = \frac{1}{2}
cos 30º = \frac{\sqrt{3}}{2}
tg 30º = \frac{\sqrt{3}}{3}
45º
sen 45º = \frac{\sqrt{2}}{2}
cos 45º = \frac{\sqrt{2}}{2}
tg 45º = 1
60º
sen 60º = \frac{\sqrt{3}}{2}
cos 60º = \frac{1}{2}
tg 60º = \sqrt{3}
Demonstração da Lei dos Senos

Nessa primeira figura vemos que a base do triângulo é c e sua altura é igual a b senα, porque ao traçarmos uma linha vertical do topo do triângulo à base, formamos dois triângulos retângulos, portanto, o cateto oposto ao ângulo alfa é igual ao produto entre o seno desse ângulo e a hipotenusa, ou seja, o valor de b.
Partindo dessas relações, construiremos as próximas equações que irão representar a área do mesmo triângulo.
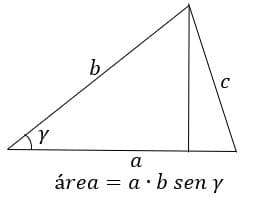
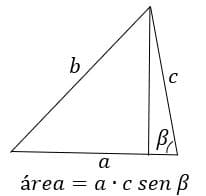
Percebam que é o mesmo triângulo e, mesmo assim, podemos escrever a sua área de diferentes formas. Desta maneira, podemos igualar todas as fórmulas.
c \cdot b \cdot sen α = a \cdot c \cdot sen β = a \cdot b \cdot senγ
Agora dividimos todos os termos por abc.
\frac {c \cdot b \cdot sen α}{abc} = \frac {a \cdot c \cdot sen β}{abc}= \frac {a \cdot b \cdot sen γ}{abc}
\frac {sen α}{a} = \frac {sen β}{b} = \frac {sen γ}{c}
Dessa forma, fica demonstrada a lei ou teorema dos senos.
Lei dos Senos no Triângulo Retângulo
Podemos encontrar algumas particularidades ao tratar dessa lei no triângulo retângulo:
(1) Um dos ângulos já conhecido, o ângulo reto, ou seja, de 90º, que a marca do triângulo retângulo e que, por sua vez, tem o seno igual a 1.
(2) Podemos facilmente estabelecer relações entre os senos e os cossenos dos seus ângulos.
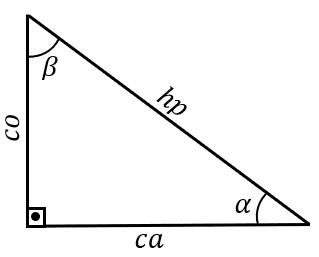
Aplicando a lei dos senos, podemos estabelecer as seguintes igualdades:
\frac {sen α}{co} = \frac {sen 90º}{hp} = \frac {sen β}{ca}
\frac {sen α}{co} = \frac {1}{hp} = \frac {sen β}{ca}
Igualando cada lado separadamente, vemos uma nova prova das relações:
\frac {sen α}{co} = \frac {1}{hp}
hp \cdot sen α = co
hp \cdot\frac {co}{hp} = co
co = co
Partindo dessas fórmulas, podemos também identificar os conceitos de seno e cosseno, quando na segunda linha, bastando dividir ambos os termos pela hipotenusa, vemos que o seno do ângulo é a razão entre o lado oposto a ele e a hipotenusa.
Proporcionalidade
Como já discutimos no início do texto, a lei nos traz uma relação de proporcionalidade entre os lados e os ângulos do triângulo. Ao analisarmos a fórmula da maneira que vimos, constatamos que um ângulo e o seu lado oposto são diretamente proporcionais, pois na medida que o lado aumenta o ângulo também aumenta, ou seja, a abertura.
Analisando cada relação de forma separada, podemos formar, a partir delas, as seguintes relações:
1) a * senβ = b * senα
2) c * senβ = b * senγ
Agora, podemos dizer que um ângulo diminui na medida que os demais lados aumentam, ou melhor, aqueles que não são o seu oposto.
Aplicação da Lei dos Senos
Diferente do que se vê no Teorema de Pitágoras, a lei dos senos se aplica a qualquer triângulo e cada uma das duas fórmulas exigem que se conheça uma quantidade de dados diferentes.
Teorema de Pitágoras
É necessário conhecer dois lados do triângulo retângulo
Lei dos Senos
Conhecer dois ângulos e um lado ou dois lados e um ângulo
Exercício de Lei dos Senos
Questão 1) Determine o ângulo β e os dois lados desconhecidos do triângulo abaixo. Considere sen 135º = 0,707, sen 30º = 0,5 e sen 15º = 0,26.
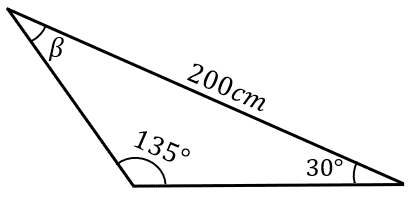
Resolução
Como já sabemos, a soma dos ângulos internos de um triângulo é sempre igual a 180º, portanto, podemos criar a seguinte relação:
135º + 30º + β = 180º
β = 180º – 135º – 30º
β = 15º
Agora, através da lei dos senos, podemos encontrar os valores dos lados não conhecidos.
\frac {sen 135º}{200} = \frac {sen 15º}{b}
b = \frac {200 \cdot sen 15º}{sen 135º}
b = \frac {200 \cdot 0,26}{0,707}
b \approx 73,55cm
\frac {sen 135º}{200} = \frac {sen 30º}{a}
a = \frac {200 \cdot sen 30º}{sen 135º}
b = \frac {200 \cdot 0,5}{0,707}
b \approx 141,44cm
Concluímos que os lados medem, aproximadamente, 73,55 cm e 141,44cm e o ângulo β é de 15º.
Questão 2) Determine a altura do triângulo equilátero abaixo através da lei dos senos.
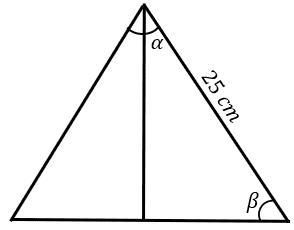
Resolução
Sendo um triângulos cujos lados são iguais, portanto, todos iguais a 25 cm, podemos dizer que os seus ângulos são também iguais. Sabendo que a soma. dos seus ângulos internos é igual a 180º, temos:
β + β + β = 180º
3β = 180º
β = 60º
Através da figura, vemos que α corresponde a metade de β, ou seja:
α = β/2
α = 60º/2
α = 30º
O ângulo oposto a β é a altura e o ângulo oposto a α é a metade do lado do triângulo, ou seja, \frac{25}{2} = 12,5. Agora que já conhecemos ângulos e lados suficientes, podemos aplicá-los a lei dos senos.
\frac {sen 30º}{12,5} = \frac {sen 60º}{h}
h = \frac {12,5 \cdot sen 60º}{sen 30º}
b = \frac {12,5 \cdot \frac{\sqrt{3}}{2}}{\frac{1}{2}}
h = 12,5\sqrt{3}
Assim, chegamos a conclusão de que a altura desse triângulo é igual a 12,5\sqrt{3}cm, ou melhor, o produto entre a metade do seu lado e \sqrt{3}.
Lei dos Cossenos
A lei dos cossenos nos permite encontrar lados ou ângulos até então desconhecidos e não se limita aos triângulos retângulos e é de fácil demonstração e uso. Nada mais agradável ao estudo matemático do que ter conhecimento das demonstrações e perspectivas para se chegar a um resultado.
Demonstração da Lei dos Cossenos
O primeiro passo para demonstrarmos a lei dos cossenos é dividirmos um triângulo qualquer em dois triângulos retângulos.
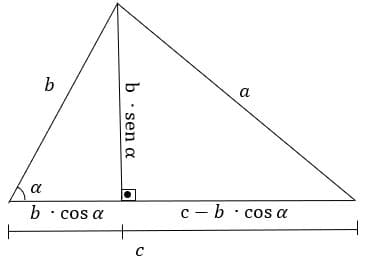
O segundo passo é relacionar os lados do triângulo retângulo da direita através do teorema de Pitágoras e das razões trigonométricas, pois ele envolve todos os lados, diferente do triângulo esquerdo, que apenas possui o valor de b. Então temos:
a^2 = {(b\cdot sen α)}^2+{(c-b\cdot cos α)}^2
a^2 = b^2\cdot sen^2 α +c^2-2cb\cdot cos α +b^2\cdot cos^2 α
a^2 = b^2(sen^2 α+cos^2 α) + c^2 -2cb\cdot cos α
a^2 = b^2+c^2 -2cb\cdot cos α
Precisamos nos atentar para uma relação, que aparece na terceira linha da demonstração e é essencial para desenvolver o cálculo.
sen^2 α+cos^2 α = \frac{co^2}{hp^2}+\frac{ca^2}{hp^2}
=\frac{co^2+ca^2}{hp^2}=\frac{hp^2}{hp^2}=1
A relação existente nessa lei funciona para qualquer um dos ângulos, caso o β (ângulo cujo lado oposto é b) seja o ângulo de referência, então teremos b^2 = a^2 + c^2-2ac\cdot cos β.
Lei dos Cossenos Fórmulas
A lei dos cossenos pode ser aplicada a qualquer triângulo onde se conheça os três lados ou dois lados e um ângulo. Conhecendo o valor de todos os lados de um triângulo é possível determinar todos os seus ângulos da seguinte forma:
Ângulo α
a^2 = b^2+c^2 -2cb\cdot cos α
a^2 -b^2-c^2= -2cb\cdot cos α
cos α=\frac{a^2 -b^2-c^2}{-2cb}
cos α=\frac{-a^2 +b^2+c^2}{2cb}
Ângulo β
b^2 = a^2+c^2 -2ac\cdot cos β
cos β=\frac{-b^2 +a^2+c^2}{2ac}
Ângulo γ
c^2 = a^2+b^2 -2ab\cdot cos γ
cos γ=\frac{-c^2 +a^2+b^2}{2ab}
Lei dos Cossenos Exercícios
1º Questão
Ao coletar os dados para um estudo topográfico da margem de um lago a partir dos pontos A, B e T, um técnico determinou as medidas AT = 32 m; BT = 13 m e ATB = 120º, representadas no esquema abaixo.

Calcule a distância, em metros, entre os pontos A e B, definidos pelo técnico nas margens desse lago.
Resolução
Aplicando a lei dos cossenos, temos:
a^2 = b^2+c^2 -2cb\cdot cos α
a^2 = {(32)}^2+{(13)}^2 -2(32)(13)\cdot cos 120º
a^2 = 1024+169 -832\cdot -\frac{1}{2}
a^2 = 1024+169 + 416
a^2 = 1609
a = \sqrt{1609}
a \approx 40
2º Questão
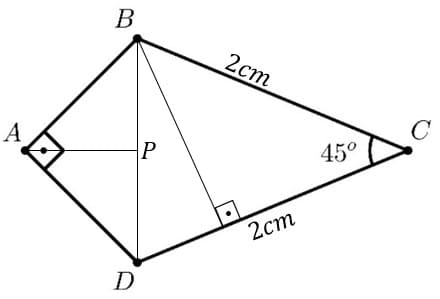
A figura abaixo exibe um quadrilátero ABCD, onde AB = AD e BC = CD = 2 cm. A área do quadrilátero ABCD é igual a
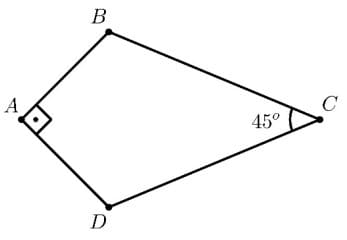
(A) \sqrt{2}cm^2
(B) 2cm^2
(C) 2\sqrt{2}cm^2
(D) 3\sqrt{2}cm^2
Resolução
O que faremos para resolver essa questão é dividir o quadrilátero em 3 triângulos e, através das relações trigonométricas fundamentais e da lei dos cossenos, encontrar os seus lados e áreas.
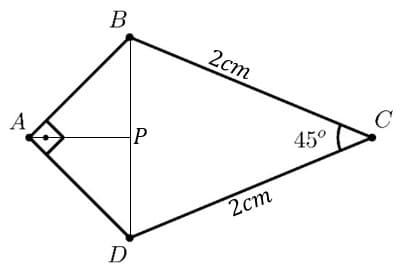
Utilizando a lei dos cossenos para encontrar o lado \overline{BD}:
Lembrando que cos 45º é \frac{\sqrt{2}}{2}
{(\overline{BD})}^2 = 2^2 +2^2 -2 \cdot 2 \cdot 2 \cdot cos 45º
=4 + 4 -8 \cdot cos 45º
=8 -8 \cdot \frac{\sqrt{2}}{2}
=8 -4 \cdot\sqrt{2}
Pela figura, vemos que as bases do triângulos ABP e ADP corresponde a metade do lado \overline{BD}. E sabemos que, possuindo um ângulo de 90º e um de 45º, o lado que falta é de45º, portanto, temos um triângulo isósceles, em outras palavras, a altura e a base são iguais. Sendo assim, a área referente aos dois triângulos menores é:
A_{ABD} =2\cdot\frac{\frac{\overline{BD}}{2}+\frac{\overline{BD}}{2}}{2}
A_{ABD} =\frac{{(\overline{BD})}^2}{4}
A_{ABD} =\frac{8 -4 \cdot\sqrt{2}}{4}
A_{ABD} =2-\sqrt{2}
Agora, traçando uma linha do ponto B até o segmento \overline{DC} formando um triângulo retângulo. Temos que a altura do triângulo BCD é:
h =2\cdot sen45º
Portanto, a área do triângulo BCD é:
A_{ABD} =\frac{2\cdot 2 \cdot \frac{\sqrt{2}}{2}}{2}= \sqrt{2}
Área do quadrilátero:
A_{ABCD} =2-\sqrt{2}+\sqrt{2}
A_{ABCD} =2
Alternativa correta – Letra B
AXLER, Sheldon. PRÉ-CÁLCULO: Uma Preparação para o Cálculo. 2. ed .Rio de Janeiro: LTC, 2016.
