Função Exponencial
Chama-se função exponencial, uma função:
Ou seja, cujo domínio seja representado por todos os números reais e o contradomínio representado por todos os números reais positivos e diferentes de zero, tal que f(n) = aⁿ para todo n ∈ IR , quando existe um número real a, com a > 0 e a ≠ 1, pois, sendo igual 1, todos os valores de f(n) seriam iguais a 1, contrariando a ideia de função.
Função Exponencial Exemplos

Gráfico da Função Exponencial
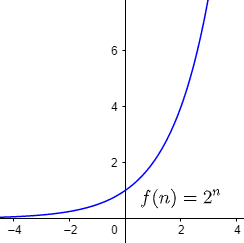
f(n) = 2ⁿ
f(n) = (1/10)ⁿ
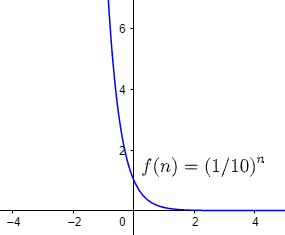
Percebemos visualmente através dos gráficos o que já discutimos sobre o contradomínio, os valores de f(n) são sempre positivos e diferentes de 0, pois não há número real que eleve outro número real resultando em 0, sendo assim ocupa sempre os quadrantes de cima, ou melhor, o primeiro e o segundo quadrante.
Todo gráfico de função exponencial intercepta o ponto (0,1), porque todo número elevado a 0 é igual a 1.
Função Exponencial Crescente e Decrescente
Uma função é descrita como crescente quando, aumentados os valores de n, o valor de f(n) também aumenta, o que acontece somente quando a > 1, pois dois números menores que 1, quando multiplicados, geram um valor ainda menor, o que pode ser visto no segundo gráfico, que representa f(n) = (1/10)ⁿ.
Exemplo de Função Decrescente
f(n) = (1/10)ⁿ
f(0) = (1/10)⁰ = 1
f(1) = (1/10)¹ = 0,1
f(2) = (1/10)² = 0,01
Exemplo de Função Crescente
f(n) = 2ⁿ
f(0) = 2⁰ = 1
f(1) = 2¹ = 2
f(2) = 2² = 4
Equações Exponenciais e Sistemas
A resolução de equações exponenciais é feita escrevendo-se ambos os lados da igualdade como potências de mesma base, como nos exemplos abaixo:
Esse raciocínio será usado para resolver questões mais complexas e que envolvam sistemas.
Exercícios Resolvidos
(Questão 1) Calcular x e y no sistema de equações abaixo:
O primeiro passo é transformar os dois lados da igualdade em potências de mesma base. Na primeira equação, optaremos por potências de base 2, enquanto na segunda optaremos por potências de base 5.
Igualando os expoente acabamos por chegar, no quarto desenvolvimento, a um novo sistema, onde é possível encontrar os valores de x e y. Substituindo a equação (2) na equação (1), temos:
Agora, iremos substituir o valor de y na equação (1) a fim de encontrar o valor de x
Chegamos ao par ordenado (4,1) como solução do nosso sistema.
Algumas questões exige que façamos algumas substituições um pouco mais complexas, o que veremos agora.
(Questão 2) Resolva a equação:
Inicialmente, iremos colocar todas as potências na mesma base. A partir do resultado, percebemos que a equação possui a estrutura de uma equação do segundo grau quando isolamos o expoente x do segundo termo a partir da propriedade da potência de uma potência. Sabendo disso, iremos dizer que y é igual a 10 elevado a x.
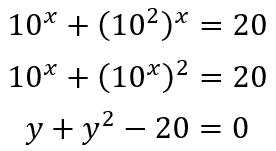
Encontramos o valor das raízes, ou seja, os valores de y.

Por último, iremos igualar as raízes a 10 elevado a x e analisar o resultados.

Das duas raízes, só uma é validade, pois toda potência de número positivo é também positiva, logo, o único valor para x será o logaritmo de 4 na base 10.
BARROSO, Juliana Matsubara. Conexões com a Matemática. 1. ed. São Paulo: Moderna, 2010
DANTE, Luiz Roberto. Matemática: contexto e aplicações. 1. ed. 3 vol. São Paulo: Ática, 2010.
3 - Monte você mesmo os seus gráficos - GeoGebra

