Função Afim para o ENEM
Ainda não entende o conceito de função? Clique aqui.
Basicamente, as questões de função afim para o Enem consistem em saber montar, através dos dados da questão, a equação abaixo. Para isso, iremos primeiro entender o que cada elemento representa separadamente e, só após, aplicá-los nas questões.
Uma função afim é dada por equação do primeiro grau, portanto, possui a seguinte estrutura:
Inclinação da Reta
A função afim é também conhecida como função linear, pois o seu gráfico é dado por uma reta, o que nos permite dizer que o seu crescimento é sempre dado em parcelas iguais. Em outras palavras, a variação é igual em qualquer ponto do gráfico, por isso, conhecendo apenas 2 pontos podemos formar uma reta, pois através de dois pontos podemos medir a variação.
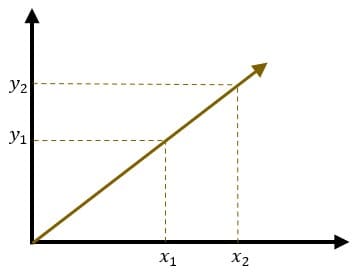
Olhando para o gráfico, vemos que, a partir do momento que a reta se desloca em relação ao eixo x, ela também se desloca para cima, mas quanto?
Podemos definir a inclinação da reta, ou coeficiente angular, como a razão entre a variação no eixo y e a variação no eixo x considerando dois pontos (x_1,y_1) e (x_2,y_2) pertencentes a reta.
Termo Independente
Estudaremos agora o valor de b, termo independente, ou coeficiente linear, são os nomes dados ao termo que não vem acompanhado de variável.
Mas o que é o coeficiente linear?
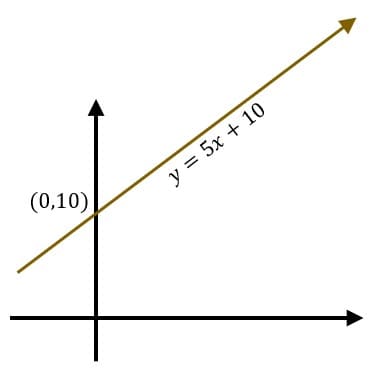
O coeficiente linear representa o ponto em que a reta corta o eixo, representa também o valor da função quando x é igual a zero. Tomemos o exemplo da equação f(x)= 5x+10. Lembrando que f(x)=y.
Ao substituirmos x por 0, encontraremos o valor de y, ou f(x), nesse ponto.
Ou seja, o ponto (0,10) pertence a reta. Isso só é possível porque todo número multiplicado por 0 é igual a zero.
Agora que já entendemos o significado de cada, iremos ver como eles são cobrados na prova do Enem.
Função Afim no ENEM
1º Questão) (Enem PPL 2017) Um sistema de depreciação linear, estabelecendo que após 10 anos o valor monetário de um bem será zero, é usado nas declarações de imposto de renda de alguns países. O gráfico ilustra essa situação.
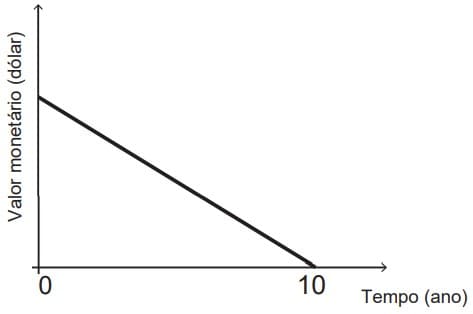
Uma pessoa adquiriu dois bens, A e B, pagando 1.200 e 900 dólares, respectivamente. Considerando as informações dadas, após 8 anos, qual será a diferença entre os valores monetários, em dólar, desses bens?
a) 30
b) 60
c) 75
d) 240
e) 300
Resolução
A questão nos pede para encontrar a diferença entre os valores dos bens após 8 anos, ou seja:
Iremos montar as funções que descrevem o processo de depreciação, em outras palavras, iremos montar a função descrita por essa reta.
Bem A
Sabemos que no tempo 0, o valor do bem A é de 1200 dólares, portanto, o coeficiente linear é de 1200.
Para encontrar o valor da inclinação, precisamos de apenas dois pontos. Usaremos os pontos (0,1200) e (10,0).
Sabemos, a partir da inclinação, que o bem sofre uma depreciação de 120 dólares ao ano.
Logo, o preço do produtos após 8 meses é:
Bem B
Coeficiente Linear: 900
Coeficiente angular (inclinação da reta):
Preço do produto B após 8 meses.
Sendo assim, a diferença entre os preços é de:
Ou seja, a alternativa correta é a letra B.
2º Questão)(Enem PPL 2017) Em um mês, uma loja de eletrônicos começa a obter lucro já na primeira semana. O gráfico representa o lucro (L) dessa loja desde o início do mês até o dia 20. Mas esse comportamento se estende até o último dia, o dia 30.
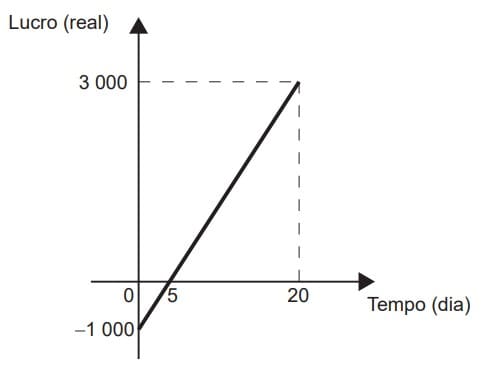
A representação algébrica do lucro (L) em função do tempo (t) é
a) L(t) = 20t + 3.000
b) L(t) = 20t + 4.000
c) L(t) 200t =
d) L(t) 200t – 1.000
e) L(t) 200t + 3.000
Resolução
Novamente iremos começar encontrando o coeficiente linear primeiro. Vemos, a partir do gráfico, que a reta corta o eixo y em -1000, ou seja, b = -1000.
Partindo de dois pontos, encontramos a inclinação. Pertencem ao gráfico os pontos (0,-1000), (5,0), (20,3000). Escolhendo os dois primeiros, temos:
Assim sendo, a representação algébrica do lucro em função do tempo é:
Alternativa correta – Letra D.
