Domínio, Contradomínio e Imagem
Função
Para entender o conceito de domínio, contradomínio e imagem precisamos entender, inicialmente, o conceito de função. Podemos definir função como um caso particular de relação entre dois conjuntos, o que irá configurar essa relação como função é o fato de que cada elemento de um conjunto A irá possuir apenas um correspondente em um conjunto B, todos dois não vazios. O que pode ser expresso através da linguagem matemática da seguinte forma:
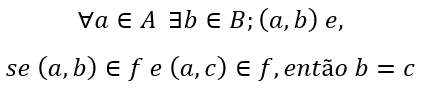
Que nos diz que para todo elemento a pertencente ao conjunto A existe um elemento b pertencente ao conjunto B. Sendo o pares (a,b) e (a,c) pertencentes a função, podemos dizer que o elemento b é igual ao elemento c, pois, para que seja uma função, não pode haver dois correspondentes no conjunto B, apenas um.
Domínio
Dada a função f de A em B ou a aplicação, transformação ou mapeamento de A em B (todos usados como sinônimo de função), chamamos A de domínio, onde um elemento qualquer do conjunto será chamado de variável independente, pois os valores correspondentes em B serão dependentes dos elementos do domínio.
Contradomínio
Nesse caso, o contradomínio é o conjunto B, melhor dizendo, onde estarão os elementos correspondentes. A partir da definição, vemos que todos os elementos do conjunto A pertencem a função, enquanto nem todos os elementos do conjunto B pertencem. Pensemos numa aplicação do conjunto dos números naturais no conjunto dos números reais, onde f(n) = 2n.
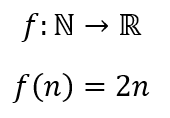
Portanto, vemos que todos os elementos correspondentes se encontram no conjunto dos números reais, porém, nem todos os elementos do conjunto são correspondentes.
Imagem
Ao conjunto dos elementos do contradomínio, conjunto B, que realmente são correspondentes, chamamos imagem. Voltando ao exemplo anterior, o conjunto Imagem seria formado pelos números naturais pares.
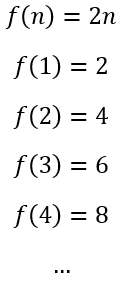
Exercícios
(Questão 1) Considere A = {0,1,2,3,4} e B = {0,2,4,9,16} e a lei b = a² que associa o elemento a de A e o elemento b de B. Essa relação é uma função? Justifique.
Não é uma função, pois o elemento 1 não possui correspondente em B.
(Questão 2) Determine o conjunto imagem das funções abaixo.

Tendo em vista o que foi estudado, sabemos que o conjunto imagem será os valores de g(x), f(x) e h(x).

(Questão 3) Determine os zeros da função.
a) f(x) = 5x – 25
b) g(x) = x³ – 8
c) p(x) = 0,25x + 4
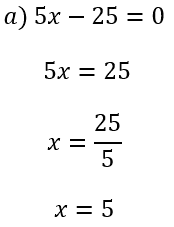
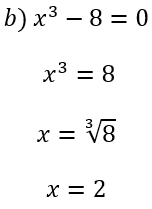

O zero da função significa o valor de x quando a imagem é igual a zero. Nesse caso, iremos igualar f(x), g(x) e p(x) a zero, encontrando os respectivos valores: 5, 2, -16.
BARROSO, Juliana Matsubara. Conexões com a Matemática. 1. ed. São Paulo: Moderna, 2010
DANTE, Luiz Roberto. Matemática. 1.ed .São Paulo: Ática, 2005.
OLIVEIRA, J. U. C. L. de. Introdução aos Princípios de Mecânica Clássica. In:_____. Função. Rio de Janeiro: LTC, 2013.
3 - Monte você mesmo os seus gráficos - GeoGebra

