Podemos definir uma progressão geométrica como uma sequência onde o cada termo é igual a divisão do termo anterior por um dado número, que será chamado de razão.
(a_1, a_1r, a_1r^2,…)
Um exemplo de progressão geométrica seria:
(1, 1 \cdot 2, 1\cdot 2 \cdot 2,…)
= (1, 2, 4,…)
Que é uma progressão geométrica de razão 2 cujo primeiro termo é 1 ou, em outros termos, uma pg de razão 2.
Termo Geral da PG
Vemos que cada termo é dado pela multiplicação de uma potência da razão da pg por um dos termos da sequência. Portanto:
a_n = a_1\cdot r^{n-1}
A existência do n-1 no expoente é justificada pelo fato de que os produtos são vistos após o primeiro termo.
Desenvolvendo essa fórmula, poderíamos escrever o termo a_5 como:
a_5 = a_1\cdot r^{4}
a_5 = a_2\cdot r^{3}
a_5 = a_3\cdot r^{2}
a_5 = a_4\cdot r^{1}
Voltando ao conceito de progressão geométrica, temos que a sua razão é dada por:
r = \frac{a_n}{a_{n-1}}
Tipos de PG
Nesse tópico, estudaremos os quatro tipos de pg:
Crescente;
Decrescente;
Constante;
Alternante.
As progressões geométricas são classificadas conforme as suas razões.
Crescente
Uma pg é crescente em duas situações:
(1) Os valores da sequência são positivos e a razão é também positiva
(1,2,4,8,16)
(2) Os valores da sequência são negativos e a razão é maior que 0 e menor que 1.
(-10,-5,\frac{-5}{2})
Decrescente
Uma pg é decrescente em duas situações:
(1) Os valores da sequência são negativos e a razão é positiva.
(-1,-2,-4,-8,-16)
(2) Os valores da sequência são positivos e a razão é maior que 0 e menor que 1.
(10,5,\frac{5}{2})
Constante
Uma progressão geométrica é constante quando a sua razão é igual a 1.
(2, 2\cdot 1, 2\cdot 1^2)
(2, 2, 2)
Alternante
Uma pg é alternante quando a sua razão é um número negativo, pois um termo n tem sempre um sinal diferente do termo n-1.
(2,-4,8,-16,32)
Soma dos Termos de uma PG Finita
Antes de apresentar a fórmula, irei apresentar a sua demonstração. Para isso, utilizaremos duas equações.
(I)\; S_n = a_1+a_2+a_3+…+a_n
qS_n = qa_1+qa_2+qa_3+…+qa_n
(II)\; qS_n = a_2+a_3+…+qa_n
Subtraindo a segunda da primeira, temos:
S_n – qS_n = a_1-qa_n
Substituindo a_n pela equação do termo geral de uma pg:
S_n – qS_n = a_1-q(a_1q^{n-1})
S_n – qS_n = a_1-a_1q^{n}
S_n(1-q) = a_1(1-q^n)
Dividindo ambos os lados por 1-q :
E assim chegamos a fórmula da soma dos termos de uma pg finita.
S_n = \frac{a_1(1-q^n)}{1-q}
Soma dos Termos de uma PG Infinita
Ao falar da soma dos termos de uma pg infinita, estamos falando das progressões geométricas que possuem uma razão cujo módulo é maior ou igual a zero. O que buscamos é uma aproximação dessa infinita soma de termos cada vez menores.
\underset {x\rightarrow \infty}{\lim} \frac{a_1(1-q^n)}{1-q}
Sabemos que quanto maior for o expoente de um número fracionário, menor ele fica, em outras palavras, ele se aproxima de zero, por isso tomaremos q^n como igual a zero.
S_n = \frac{a_1(1-0)}{1-q}
S_n = \frac{a_1}{1-q}
PG no ENEM
Questão 1 – ENEM 2015 PPL ) O padrão internacional ISO 216 define os tamanhos de papel utilizados em quase todos os países. O formato-base é uma folha retangular de papel chamado de A0, cujas dimensões estão na razão 1:√2. A partir de então, dobra-se a folha ao meio, sempre no lado maior, definindo os demais formatos, conforme o número de dobradura. Por exemplo, A1 é a folha A0 dobrada ao meio uma vez, A2 é a folha A0 dobrada ao meio duas vezes, e assim sucessivamente, conforme figura:

Q Um tamanho de papel bastante comum em escritórios brasileiros é o A4, cujas dimensões são 21,0 cm por 29,7cm.
Quais são as dimensões, em centímetros, da folha A0?
(A) 21,0 x 118,8
(B) 84,0 x 29,7
(C) 84,0 x 118,8
(D) 168,0 x 237,6
(E) 336,0 x 475,2
Resolução
Sabemos que até o papel é dobrado sempre no lado maior, por isso, cada lado é reduzido pela metade duas vezes até se tornar uma folha A4. Bastaria multiplicarmos as medidas da folha A4 por 4 para encontrarmos as medidas da folha A0, mas faremos através do conceito de progressão geométrica.
(a, \frac{a}{2}, 21,0)
a_3 = a_1r^2
a_1 = \frac{a_3}{r^2}
a_1 = \frac{a_3}{{(\frac{1}{2})}^2}
a_1 = \frac{21}{\frac{1}{4}}
a_1 = 84
(b, \frac{b}{2}, 29,7)
b_1 = \frac{29,7}{\frac{1}{4}}
b_1 = 118,8
Questão 2 – ENEM 2020 ) O artista gráfico holandês Maurits Cornelius Escher criou belíssimas obras nas quais as imagens se repetiam, com diferentes tamanhos, induzindo ao raciocínio de repetição infinita das imagens. Inspirado por ele, um artista
fez um rascunho de uma obra na qual propunha a ideia de construção de uma sequência de infinitos quadrados, cada vez menores, uns sob os outros, conforme indicado na figura.
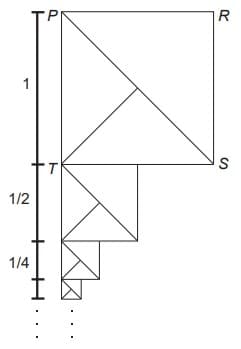
O quadrado PRST, com lado de medida 1, é o ponto de partida. O segundo quadrado é construído sob ele tomando-se o ponto médio da base do quadrado anterior e criando-se um novo quadrado, cujo lado corresponde à metade dessa base. Essa sequência de construção se repete recursivamente. Qual é a medida do lado do centésimo quadrado construído de acordo com esse padrão?
Resolução
Identificando a razão da pg através da divisão entre um termo e seu anterior, descobrimos que a razão é \frac{1}{2}.
Utilizando a fórmula do termo geral da pg:
a_n=a_1r^{n-1}
a_{100}= 1\cdot {(\frac{1}{2})}^{100-1}
a_{100}= {(\frac{1}{2})}^{99}
