O conteúdo de estatística para o ENEM (Exame Nacional do Ensino Médio) se baseia basicamente no estudo de dados apresentados em gráficos e dos conceitos de média aritmética, moda e mediana.
Média Aritmética
A média aritmética consiste no valor dado pelo razão entre o somatório de um conjunto de termos pelo número de elementos somados, ou seja:
Valendo-se o símbolo do somatório:
Que significa o somatório dos valores de x sabendo que o índice i varia de 1 a n, ou seja, soma-se todos os valores de x indo do primeiro ao último termo, em outras palavras, até n.
Média Aritmética Ponderada
Ao calcular a média anterior, admitimos que todos os valores tem o mesmo peso. Vejamos como calcular a média aritmética quando os pesos são diferentes.
Tomemos o ENEM como exemplo, vamos supor que uma certa faculdade atribui os seguintes pesos para cada área do conhecimento:
Linguagens, Códigos e suas Tecnologias – 1
Matemática e suas Tecnologias – 3
Ciências Humanas e suas Tecnologias – 2,5
Ciências da Natureza e Suas Tecnologias -1,5
Redação – 2
Agora, vamos admitir que um certo aluno obteve as seguintes pontuações:
Linguagens, Códigos e suas Tecnologias – 750
Matemática e suas Tecnologias – 900
Ciências Humanas e suas Tecnologias – 830
Ciências da Natureza e Suas Tecnologias – 800
Redação – 720
Qual a média obtida por esse aluno?
Diferente da média aritmética simples, na média ponderada iremos multiplicar cada termo por seu respectivo peso e, após isso, dividir a soma desses valores pela soma dos pesos. Voltando ao nosso exemplo:
A média, ou seja, a nota final do aluno seria de 812,5 pontos.
Média no Enem
1º Questão – Enem 2018) De acordo com um relatório recente da Agência Internacional de Energia (AlE), o mercado de veículos elétricos atingiu um novo marco em 2016, quando foram vendidos mais de 750 mil automóveis da categoria. Com isso, o total de carros elétricos vendidos no mundo alcançou a marca de 2 milhões de unidades desde que os primeiros modelos começaram a ser comercializados em 2011. No Brasil, a expansão das vendas também se verifica. A marca A, por exemplo, expandiu suas vendas no ano de 2016, superando em 360 unidades as vendas de 2015, conforme representado no gráfico.
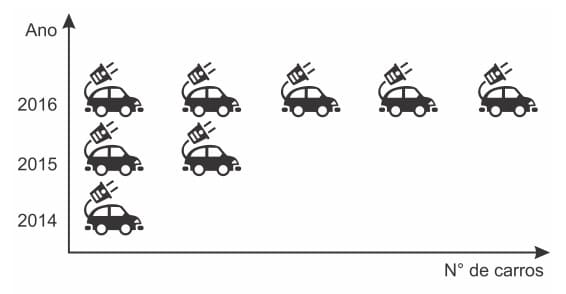
A média anual do número de carros vendidos pela marca A, nos anos representados no gráfico, foi de
a) 192
b) 240
c) 252
d) 320
e) 420
Resolução
O gráfico nos mostra o número de carros vendidos pela marca A nos anos de 2014, 2015 e 2016 onde cada carro representa uma certa quantidade de vendas. Sabemos, a partir do enunciado, que a diferença entre 2015 e 2016 foi de 360 unidades e pelo gráfico vemos que a diferença é de 3 carros. Logo, cada carro representa:
Voltando ao conceito de média, precisamos apenas saber o número de vendas dos 3 anos, somá-los e dividi-los por 3.
Por isso, a alternativa correta é a letra D.
Moda
A moda tem o objetivo de indicar um certo tipo de tendência. Em estatística, a moda significa o valor com maior frequência, ou seja, aquele que mais se repete. Exemplo:
Foram feitos 10 pedidos de camisetas a uma de certa loja, os tamanhos das camisetas pedidas são os seguintes:
M, P, M, G, G, PP, G, P, G, G.
Ao analisarmos as frequências dos tamanhos, vemos que foram pedidas 2 camisetas de tamanho M, 2 camisetas de tamanho P, 1 camiseta de tamanho PP e 5 camisetas de tamanho G.
Como a moda significa o valor com maior frequência, a moda desse problema é G.
Mediana
A mediana também é um indicador de tendência e irá representar o valor central quando os números são colocados em ordem crescente ou decrescente. Por exemplo:
5 alunos são selecionados em uma turma do 1º ano do ensino médio e as suas alturas são:
1,75 ; 1,80 ; 1,56; 1,72 ; 1,68.
Para encontrar a mediana precisamos, primeiramente, colocar esses valores em ordem, colocaremos em ordem crescente.
1,56 ; 1,68 ; 1,72 ; 1,75 ; 1,80.
A mediana é 1,72, pois esse se encontra no centro.
E se o número de termos fosse par?
1,56 ; 1,68 ; 1,72 ; 1,74 ; 1,75 ; 1,80.
A mediana seria dada pela média aritmética dos dois termos centrais, nesse caso:
M_e = \frac{1,72+1,74}{2} = 1,73Exercícios ENEM Média, Moda e Mediana
1º Questão)(Enem 2019) Os alunos de uma turma escolar foram divididos em dois grupos. Um grupo jogaria basquete, enquanto o outro jogaria futebol. Sabe-se que o grupo de basquete é formado pelos alunos mais altos da classe e tem uma pessoa a mais do que o grupo de futebol. A tabela seguinte apresenta informações sobre as alturas dos alunos da turma.
Média – 1,65
Mediana – 1,67
Moda – 1,70
Os alunos P, J, F e M medem, respectivamente, 1,65 m,1,66 m,1,67 m e 1,68 m, e as suas alturas não são iguais a de nenhum outro colega da sala. Segundo essas informações, argumenta-se que os alunos P, J, F e M jogaram, respectivamente,
a) basquete, basquete, basquete, basquete
b) futebol, basquete, basquete, basquete
c) futebol, futebol, basquete, basquete
d) futebol, futebol, futebol, basquete
e) futebol, futebol, futebol, futebol
Resolução
A partir do conceito de mediana, sabemos que ela representa o termo do centro, quando os dados são colocados em ordem e sabendo que há um número ímpar de jogadores, pois um time tem um número ímpar e outro tem um número par, podemos dizer que a mediana corresponde há um termo que pertence ao conjunto, ou seja, 1,67.
Como o maior time é o de basquete, porque possui um jogador a mais, logo, aquele que possuir a altura a qual corresponde a mediana, joga no time de basquete.
Ou seja, os 2 primeiros jogadores fazem parte do time de futebol, enquanto os demais fazem parte do time de basquete. Alternativa correta – Letra C.
2º Questão)(Enem PPL 2017) Numa turma de inclusão de jovens e adultos na educação formal profissional (Proeja), a média aritmética das idades dos seus dez alunos é de 32 anos. Em determinado dia, o aluno mais velho da turma faltou e, com isso, a média aritmética das idades dos nove alunos presentes foi de 30 anos. Qual é a idade do aluno que faltou naquela turma?
a) 18
b) 20
c) 31
d) 50
e) 62
Resolução
A turma possui 10 alunos e apresenta uma média de 32 anos, ou seja:
isolando a somatório
Sabemos que a soma das idades é igual 320, portanto, a idade do aluno que saiu é:
Alternativa correta – LETRA D.
1 - Provas ENEM
