1ª Propriedade
O determinante será igual a zero nos seguintes casos:
Podemos afirmar que a determinante de uma matriz é igual a zero analisando pontos específicos.
(1) Caso uma das linhas ou colunas seja igual a zero.
Daremos preferência a Regra de Sarrus para demonstrar as propriedades.
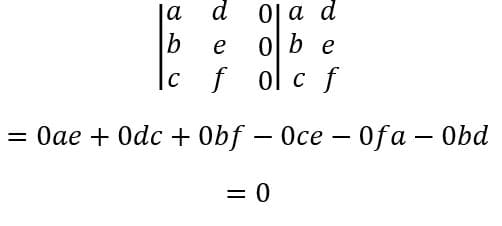
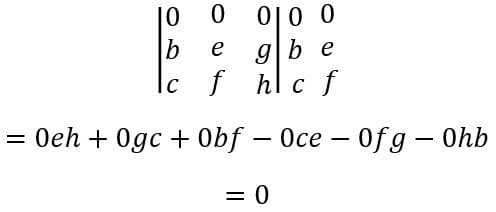
Percebemos então que a presença de uma coluna ou linha nula gera um determinante também nulo.
(2) Caso duas linhas ou colunas sejam idênticas ou proporcionais
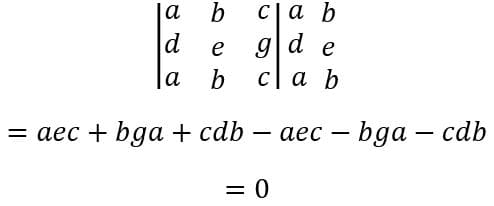
O mesmo vale para caso se tenha duas colunas iguais.
Em linhas proporcionais, temos a mesma relação que a apresentada acima, porém agora os resultados obtidos são multiplicados por um número tal, no exemplo abaixo temos o número 2, pois a linha 3 é o dobro da linha 2. ou seja, (L1)*2 = L3. O mesmo vale para as colunas.
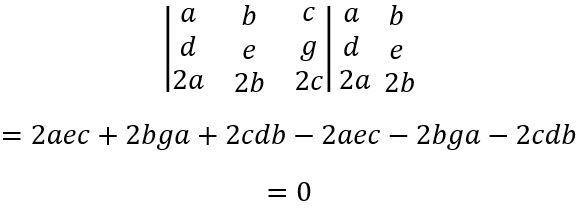
(3) Em casos em que a matriz possui uma linha ou coluna que é uma combinação linear das outras linhas ou das outras colunas, respectivamente.
Iremos ter uma combinação linear quando pudermos escrever uma linha ou coluna tal da seguinte forma:
Para provar, faremos da terceira linha de uma matriz qualquer uma combinação linear das outras duas.
Ainda usando a Regra de Sarrus, temos:
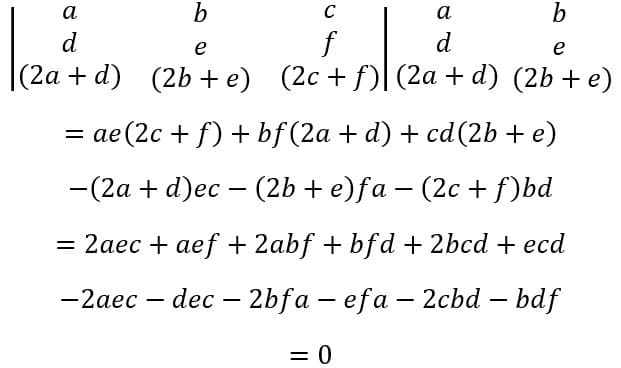
2ª Propriedade
O determinante de uma matriz é igual ao determinante da sua transposta
Para encontrar a transposta de uma matriz basta que façamos das linhas colunas ou das colunas linhas.
A partir de uma análise visual da transposta vemos que os elementos das diagonais principal e secundária se mantêm constantes, deles inverte-se apenas o valor das posições 3×1 e 1×3.
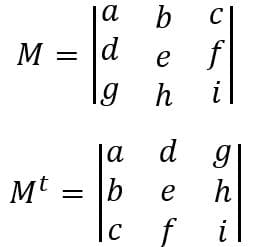
Calculando as determinantes temos:
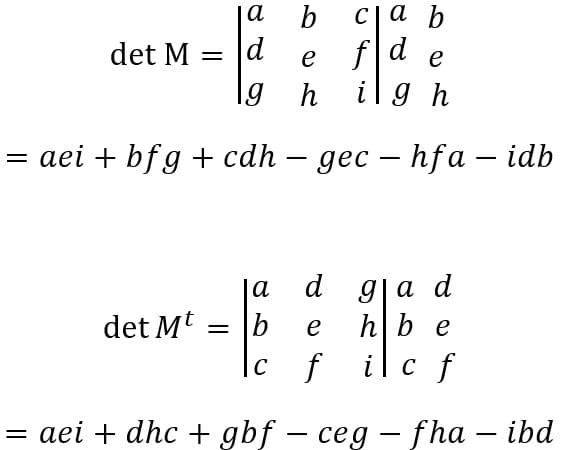
3ª Propriedade
inverter duas linhas ou colunas resulta em uma matriz de determinante contrário.
Inverteremos a primeira e a segunda linha.
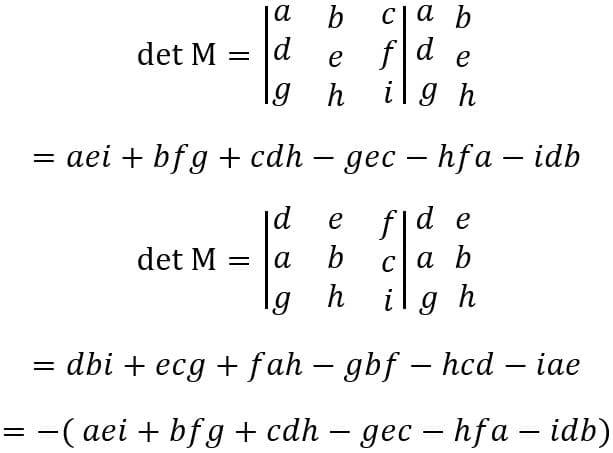
Invertendo-se duas linhas ou colunas, os termos que apareciam na diagonal principal aparecem agora na diagonal secundária, consequentemente, o sinal da determinante será contrário.
Na demonstração é importante se atentar a ordem das multiplicações.
4ª Propriedade
Somar a uma linha uma combinação linear das outras duas gera uma matriz de mesmo determinante ( Teorema de Jacobi )
A partir de tal proposição podemos voltar a primeira propriedade ( item 3 ) e deduzir que é possível zerar uma das linhas, subtraindo-a por uma combinação linear das outras, já que são proporcionais.
Quer conhecer uma aplicação de determinantes na condição de alinhamento de três pontos? Clique aqui.
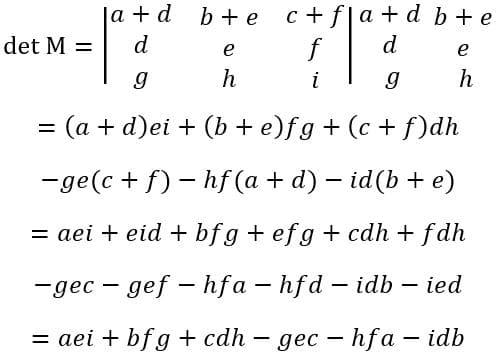
Somei à primeira linha a segunda, que é uma combinação linear da seguinte forma:
Com o acréscimo da segunda linha a primeira, a determinante foi igual a calculada anteriormente.
Convido o leitor a averiguar usando a fórmula genérica para a combinação linear.
5ª Propriedade
Para matrizes quadradas de mesma ordem O produto dos determinantes é igual o determinante do produto das matrizes (Teorema de Binet)
Iremos arbitrar valores para duas matrizes A e B e averiguar a propriedade
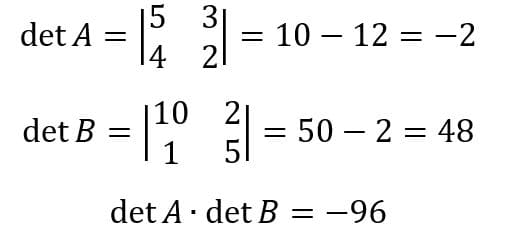
Multiplicando separadamente cada determinante obtemos o valor -96.
Agora multiplicaremos as matrizes e então encontramos seu determinante.
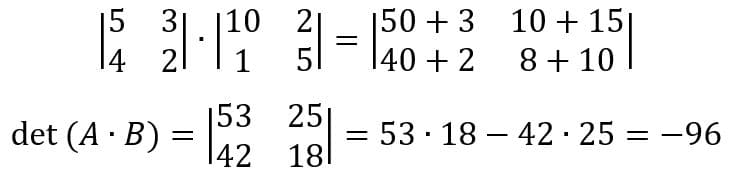
Assim como na situação anterior, o determinante foi igual a -96.
Caso ainda não saiba multiplicar matrizes Clique aqui.
6ª Propriedade
Matrizes do tipo triangular, diagonal e identidade possuem seu determinante igual ao produto dos termos da diagonal principal
Caso ainda não conheça os tipos de matrizes Clique aqui.
O que confirma a proposição é o fato de que essas matrizes possuem os números acima ou abaixo da diagonal principal iguais a zero.
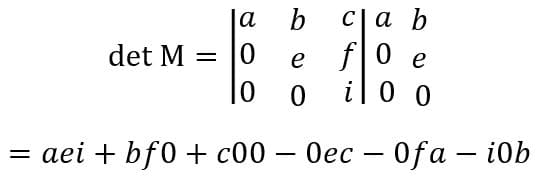
Na figura acima vemos o cálculo da determinante de uma matriz triangular e percebemos que os termos nulos fazem com que todas as diagonais calculadas a partir da regra de Sarrus tenham os produto dos seus elementos igual a zero, menos a principal.
7ª Propriedade
caso multipliquemos todos os elementos de uma linha ou de uma coluna por um número n, então seu determinante será também multiplicada por n.
Podemos averiguar visualmente através dos outros exemplos que cada termo que será multiplicado por um valor n aparece uma vez nos valores positivos e uma nos valores negativos usando a regra de Sarrus.
Abaixo testaremos a propriedade em uma matriz 2×2, multiplicando a primeira linha por 2 temos:
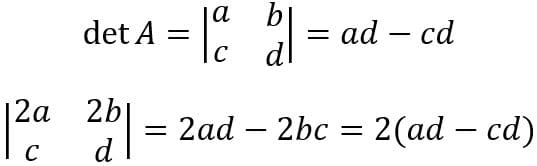
RIBEIRO, Jackson. Matemática: ciência, linguagem e tecnologia, 2. São Paulo: Scipione, 2010.
FILHO, Benigno Barreto ; SILVA, Claudio Xavier. Matemática aula por aula. 2. ed. São Paulo: FTD, 2005:

