O conceito de proporção depende do conceito de razão. Enquanto razão é a divisão entre dois números ou grandezas, proporção é uma igualdade existente entre razões. Esses conceitos são apresentados no Enem junto a conceitos como vazão, densidade, escala, entre outros.
Razão
Lembrando que uma razão é um divisão, costumamos a escrever de duas maneiras:
Exemplo: Em uma horta havia 200 pés de alface, foram retirados 50 para venda, qual a razão entre o números de pés retirados e o número de pés que a horta tinha?
Aplicações do Conceito de Razão
Escala
Uma escala representa a razão entre a medida da miniatura e a medida real.
Exemplo: Em um mapa de uma pequena cidade, destaca-se a presença de uma rodovia, cuja extensão é de 20 quilômetros. No mapa em questão, sua medida é de 10 centímetros, o que nos permite concluir que a sua escala cartográfica é de:
Simplificando a expressão dividindo numerador e denominador por 10, temos:
Sabendo que a notação mais comum para escala é a segunda forma que vimos de como escrever uma razão.
Vazão
A vazão significa a quantidade de volume que passa por uma seção em um determinado tempo, ou seja:
e umas das suas medidas convencionais são:
Razão no ENEM
1º Questão)(ENEM 2021) Após o término das inscrições de um concurso, cujo número de vagas é fixo, foi divulgado que a razão entre número de candidatos e o número de vagas, nesta ordem, era igual a 300. Entretanto, as inscrições foram prorrogadas, inscrevendo-se mais 4000 candidatos, fazendo com que a razão anteriormente referida passasse a ser igual a 400. Todos os candidatos inscritos fizeram a prova, e o total de candidatos aprovados foi igual à quantidade de vagas, Os demais candidatos foram reprovados. Nessas condições, quantos foram os candidatos reprovados?
a) 11.960
b) 11.970
c) 15.960
d) 15.970
e) 19.960
Resolução
O primeiro passo em uma questão como essa é identificar os dados que podem ser escritos como equações. Vamos ao primeiro:
a razão entre número de candidatos e o número de vagas, nesta ordem, era igual a 300
Partindo do conceito de razão:
segundo trecho:
inscrevendo-se mais 4000 candidatos, fazendo com que a razão anteriormente referida passasse a ser igual a 400
A partir dessas duas equações, podemos encontrar os valor de c (candidatos inscritos inicialmente) e v (número de vagas).
Substituindo a equação (I) na equação (II), temos:
Portanto, foram ofertadas 40 vagas. Substituindo o valor de v na equação (I)
Sabendo que foram inscritas 16.000 pessoas, pois 12.000 + 4.000 = 16.000, o número de pessoas reprovadas foi:
Ou seja, a alternativa correta é a letra C.
Proporção
Como já foi discutido, uma proporção representa uma igualdade entre razões:
e lê-se da seguinte forma:
a está para b assim como c está para d
Em uma proporção, o produto dos meios é igual ao produto dos extremos, essa nomenclatura é mais facilmente visualizada quando vemos esses valores escritos na segunda forma da razão.
Fazendo-se as devidas operações:
Números e Grandezas Diretamente Proporcionais
Grandezas são diretamente proporcionais quando a razão entre elas é constante.
a e b, assim como c e d, são números diretamente proporcionais pois cada crescimento de um representa também um crescimento do outro. E suas razões são iguais a k, uma constante.
Números e Grandezas Inversamente Proporcionais
Um número a é inversamente proporcional a b se, e somente se, a for diretamente proporcional ao inverso de b.
Proporção no ENEM
1º Questão)(ENEM 2016) Para a construção de isolamento acústico numa parede cuja área mede
9m^2,sabe-se que, se a fonte sonora estiver a 3m do plano da parede, o custo é de R$ 500,00. Nesse tipo de isolamento, a espessura do material que reveste a parede é inversamente proporcional ao quadrado da distância até a fonte sonora, e o custo é diretamente proporcional ao volume do material do revestimento. Uma expressão que fornece o custo para revestir uma parede de área A (em metro quadrado), situada a D metros da fonte sonora, é
a) \frac{500\cdot 81}{A \cdot D^2}
b) \frac{500\cdot A}{D^2}
c) \frac{500\cdot D^2}{A^2}
d) \frac{500\cdot A\cdot D^2}{81}
e) \frac{500\cdot 3 \cdot D^2}{A}
Resolução
Assim como na questão anterior, iremos destacar os trechos que podem ser transformados em equações.
a espessura do material que reveste a parede é inversamente proporcional ao quadrado da distância até a fonte sonora
custo é diretamente proporcional ao volume do material do revestimento
Sabemos que o volume é o produto entre a área e a espessura, portanto:
Precisamos de uma fórmula que apresente o custo, a área e a distância da fonte sonora. Para isso, iremos substituir a equação (I) na equação (II)
Falta-nos descobrir o valor das constantes, para isso, iremos substituir os demais valores que são dados no seguinte trecho:
Para a construção de isolamento acústico numa parede cuja área mede 9m^2,sabe-se que, se a fonte sonora estiver a 3m do plano da parede, o custo é de R$ 500,00
Substituindo esse valor na fórmula que encontramos:
Alternativa correta – Letra C
2º Questão)(ENEM 2018) Um mapa é a representação reduzida e simplificada de uma localidade. Essa redução, que é feita com o uso de uma escala, mantém a proporção do espaço representado em relação ao espaço real. Certo mapa tem escala 1: 58.000.000.
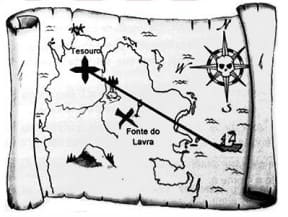
Considere que, nesse mapa, o segmento de reta que liga o navio à marca do tesouro meça 7,6 cm. A medida real, em quilômetro, desse segmento de reta é
a) 4.408
b) 7.632
c) 44.080
d) 76.316
e) 440.800
Resolução
Sabemos que uma escala é a razão entre a medida no mapa e a medida real e sabemos também que são números proporcionais, logo:
Sabemos que, ao escrever uma escala, a medida do mapa e a medida real devem ser iguais, portanto, 7,6 cm no mapa representa 440.800.000cm, ou:
Letra A.
2º Questão)(ENEM 2018) Um mapa é a representação reduzida e simplificada de uma localidade. Essa redução, que é feita com o uso de uma escala, mantém a proporção do espaço representado em relação ao espaço real. Certo mapa tem escala 1: 58.000.000.
1 - Provas ENEM
