O logaritmo é uma forma de lidar com variáveis no expoente e possui um conjunto de propriedades, que quando conhecidas, tornam o estudante capaz de manipular as equações para encontrar uma solução. E o conjunto dessas propriedades do logaritmo, para o ENEM, não é grande, mas exige domínio. De maneira geral, um logaritmo significa:
Exemplos
Propriedade das Operações
Estudaremos um conjunto de pequenas propriedades relacionadas as operações, que quando bem dominadas e desenvolvidas, respondem qualquer questão que envolva logaritmo, pois elas permitem simplificar e alterar o logaritmo e assim poder substituir pelos valores dados nas questões ou apenas reduzir para logaritmos mais simples.
1º propriedade - Logaritmo de um produto
2º propriedade - Logaritmo de um quociente
3º propriedade - Logaritmo de uma potência
4º propriedade - Mudança de base
Propriedades Secundárias
Mesmo que bastante intuitivas ou pouco frequentes, tais propriedades possuem a sua importância e facilitarão o desenvolvimento dos cálculos.
Propriedade (a)
\log_a 1 = 0 e \log_a a = 1
Propriedade (b)
Propriedade (c)
Questões de Logaritmo do Enem
1º Questão) A Lei de Zipf, batizada com o nome do linguista americano George Zipf, é uma lei empírica que relaciona a frequência (f) de uma palavra em um dado texto com o seu ranking (r). Ela é dada por
O ranking da palavra é a sua posição ao ordenar as palavras por ordem de frequência. Ou seja, r=1 para a palavra mais frequente, r=2 para a segunda palavra mais frequente e assim sucessivamente. A e B são constantes positivas.
Com base nos valores de X = log (r) e Y = log (f), é possível estimar valores para A e B.
No caso hipotético em que a lei é verificada exatamente, a relação entre Y e X é:
a) Y = log (A)-B\cdot X
b) Y=\frac{log (A)}{X+log (B)}
c) Y=\frac{log (A)}{B}-X
d) Y=\frac{log (A)}{B\cdot X}
e) Y=\frac{log (A)}{X^B}
Resolução
O primeiro passo consiste em reconhecer que é possível formar logaritmos em ambos os lados, veremos o porquê.
10^N= f e 10^N=\frac{A}{r^B}
portanto
Agora que já entendemos que é possível usar o log dos dois lados, vamos prosseguir com o desenvolvimento.
Utilizando a segunda propriedade:
Usando a terceira propriedade:
Substituindo log f por Y e log r por X, temos:
Logo, a alternativa correta é a letra A.
2º Questão) Charles Richter e Beno Gutenberg desenvolveram a escala Richter, que mede a magnitude de um terremoto. Essa escala pode variar de 0 a 10, com possibilidades de valores maiores. O quadro mostra a escala de magnitude local (M_s) de um terremoto que é utilizada para descrevê-lo.
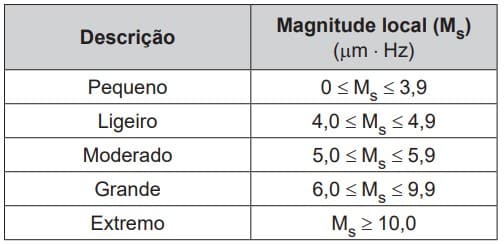
Para se calcular a magnitude local, usa-se a fórmula Ms = 3,30 + log(A⋅f), em que A representa a amplitude máxima da onda registrada por um sismógrafo em micrômetro (µm) e f representa a frequência da onda,
em hertz (Hz). Ocorreu um terremoto com amplitude máxima de 2 000 µm e frequência de 0,2 Hz. Utilize 0,3 como aproximação para log 2.
De acordo com os dados fornecidos, o terremoto ocorrido pode ser descrito como:
a) Pequeno
b) Ligeiro
c) Moderado
d) Grande
e) Extremo
Resolução
Dessa vez, a questão nos deu uma fórmula que já contém o logaritmo, o que precisamos fazer é substituir as variáveis pelo valores dados no enunciado e fazer as devidas operações:
A amplitude máxima e a frequência já se encontram nas medidas adequadas, logo, basta substituir.
Ao dividir o 400 em um produto, podemos transformar esse log numa soma de dois logaritmos.
Utilizando a terceira fórmula:
Substituindo log 2 por 0,3, temos:
A partir da tabela, vemos que a magnitude local foi moderada, portanto, a alternativa correta é a letra C.
DANTE, Luiz Roberto. Matemática. 1.ed .São Paulo: Ática:2005
