Podemos definir uma progressão aritmética como uma sequência onde o cada termo é igual a soma do termo anterior mais um dado número padrão, que será chamado de razão.
Um exemplo de progressão aritmética seria:
Que é uma progressão aritmética de razão 3 cujo primeiro termo é 1.
Fórmula da Progressão Aritmética
Transformando o raciocínio visto anteriormente em uma equação, dizemos que o termo geral da pa (progressão aritmética) é:
A partir da fórmula, sabemos que o enésimo termo representa a soma entre o primeiro termo da pa e a razão correspondente.
Admitindo que o primeiro termo da pa é o termo 0, temos:
As duas fórmulas são válidas e dependem da preferência do aluno.
Logo, a razão da progressão aritmética é dada pela diferença entre um certo termo da sequência e o seu anterior.
Exercícios de Progressão Aritmética
1º Questão) Encontre o termo geral da pa abaixo:
Sabemos que a razão é dada pela diferença entre um termo e o seu anterior, por isso:
Substituindo na fórmula do termo geral:
2º Questão) Determine o 10º termo de uma progressão aritmética de razão 5 cujo segundo termo é -8.
Se o segundo termo é -8, sabemos que o primeiro termo é -13, logo, a partir da fórmula do termo geral da pa, temos:
Soma Progressão Aritmética
O raciocínio por trás da soma dos termos de uma pa consiste em perceber que a soma entre o primeiro termo e o último termo é igual a soma do segundo termo pelo penúltimo e assim sucessivamente. Vamos a um exemplo sendo n o último termo.
Portanto, a soma dos termos dessa pa é 35\cdot 3=105. Que em resumo, é o produto entre a soma dada pelo primeiro e último termo e a metade do número de termos, ou seja:
Progressão Aritmética Enem
1º Questão) (Enem (Libras) 2017) A figura ilustra uma sequência de formas geométricas formadas por palitos, segundo uma certa regra. Continuando a sequência, segundo essa mesma regra, quantos palitos serão necessários para construir o décimo termo da sequência?

Continuando a sequência, segundo essa mesma regra, quantos palitos serão necessários para construir o décimo termo da sequência?
a) 30
b) 39
c) 40
d) 43
e) 57
Resolução
Sabemos que a primeira forma foi feita com 3 palitos, a segunda com 7 e a terceira com 11, ou seja, temos uma progressão aritmética de razão 4 cujo primeiro termo é 3.
Alternativa correta – Letra B
2º Questão)(Enem 2016) Sob a orientação de um mestre de obras, João e Pedro trabalharam na reforma de um edifício. João efetuou reparos na parte hidráulica nos andares 1, 3, 5, 7, e assim sucessivamente, de dois em dois andares. Pedro trabalhou na parte elétrica nos andares 1, 4, 7, 10, e assim sucessivamente, de três em três andares. Coincidentemente, terminaram seus trabalhos no último andar. Na conclusão da reforma, o mestre de obras informou, em seu relatório, o número de andares do edifício. Sabe-se que, ao longo da execução da obra, em exatamente 20 andares, foram realizados reparos nas partes hidráulica e elétrica por João e Pedro. Qual é o número de andares desse edifício?
a) 40
b) 60
c) 100
d) 115
e) 120
Resolução
Estudando a sequência, vemos que eles realizaram reparos juntos nos andares 1,7,13…
Vemos que essa sequência forma uma pa de razão 6 e tem seu primeiro termo igual a 1.
Sabendo que o último andar passou por reformas tanto de João quanto de Pedro e que 20 andares foram obtiveram reparos de ambos.
Alternativa correta – Letra D
3º Questão)(Enem 2013) As projeções para a produção de arroz no período de 2012– 2021, em uma determinada região produtora, apontam para uma perspectiva de crescimento constante da produção anual. O quadro apresenta a quantidade de arroz, em toneladas, que será produzida nos primeiros anos desse período, de acordo com essa projeção.
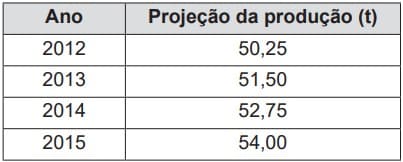
A quantidade total de arroz, em toneladas, que deverá ser produzida no período de 2012 a 2021 será de
a) 497,25
b) 500,85
c) 502,87
d) 558,75
e) 563,25
Resolução
Razão:
Produção em 2021:
Soma dos termos da progressão aritmética:
Alternativa correta – Letra D
